Eckmann–Hilton argument

For the notion of duality in algebraic topology, see Eckmann–Hilton duality.

In mathematics, the Eckmann–Hilton argument (or Eckmann–Hilton principle or Eckmann–Hilton theorem) is an argument about two monoid structures on a set where one is a homomorphism for the other. Given this, the structures can be shown to coincide, and the resulting monoid demonstrated to be commutative. This can then be used to prove the commutativity of the higher homotopy groups. The principle is named after Beno Eckmann and Peter Hilton, who used it in a 1962 paper.

1 The Eckmann–Hilton result
2 Remarks
3 Proof
4 References
5 External links

The Eckmann–Hilton result

Let $X$ be a set equipped with two binary operations, which we will write . and *, and suppose:

1. * and . are both unital, with the same unit 1, say, and
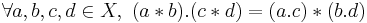2. $\forall a,b,c,d \in X,\ (a*b).(c*d) = (a.c)*(b.d)$ .

Then * and . are the same and in fact commutative.

Remarks

The operations * and . are often referred to as multiplications, but this might imply they are associative, a property which is not required for the proof. In fact associativity follows; moreover, condition 1 above can be weakened to the assertion that both operations are unital, since it can be proved from condition 2 that the units must then coincide. 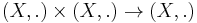If the operations are associative, each one defines the structure of a monoid on $X$ , and the conditions above are equivalent to the more abstract condition that * is a monoid homomorphism $(X,.)\times(X,.)\to(X,.)$ (or vice versa). An even more abstract way of stating the theorem is: If $X$ is a monoid object in the monoidal category of monoids, then $X$ is in fact a commutative monoid.

Proof

The proof is not hard, although it is much more conceptually clear if geometric diagrams are used. In ordinary algebra notation, the proof is as follows:

Let 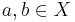$a,b \in X$ . Then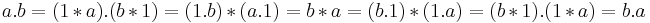 $a.b = (1*a).(b*1) = (1.b)*(a.1) = b*a = (b.1)*(1.a) = (b*1).(1*a) = b.a \,$

It is sometimes represented as a 'clock'. In this image, "0" is the unit for p⊕q and "1" is the unit for ⊗. Starting from any position on the clock we can move to the next by some use of the unital character of "0" and "1" or the distributive rule:

References

John Baez: Eckmann–Hilton principle (week 89)
John Baez: Eckmann–Hilton principle (week 100)
Eckmann, B.; Hilton, P. J. (1962), "Group-like structures in general categories. I. Multiplications and comultiplications", Mathematische Annalen 145: 227–255, MR 0136642 .

External links

Eugenia Cheng of 'the Casters' video team explains the Eckmann Hilton argument.