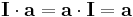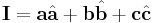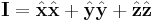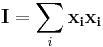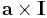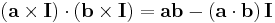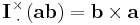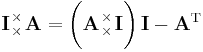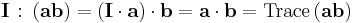Dyadics

Dyadics are mathematical objects, representing linear functions of vectors. Dyadic notation was first established by Gibbs in 1884.

1 Definition
2 Dyadics algebra
3 See also
4 References

Definition

Dyad A is formed by two vectors a and b (complex in general). Here, upper-case bold variables denote dyads (as well as general dyadics) whereas lower-case bold variables denote vectors.

$\mathbf{A}= \mathbf{a}\mathbf{b}$

In matrix notation :

$\mathbf{A} = \mathbf{a}\mathbf{b}^\mathrm{T} = \left( \begin{array}{c} a_1 \\ a_2 \end{array} \right)\left( \begin{array}{cc} b_1 & b_2 \end{array} \right) = \left( \begin{array}{cc} a_1b_1 & a_1b_2 \\ a_2b_1 & a_2b_2 \end{array} \right).$

In general algebraic form:

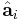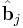$\mathbf{A} = \sum _{i,j} a_{i}b_{j}\hat{\mathbf{a}}_i\hat{\mathbf{b}}_j$

where $\hat{\mathbf{a}}_i$ and $\hat{\mathbf{b}}_j$ are unit vectors (also known as coordinate axes) and i,j goes from 1 to the space dimension.

A dyadic polynomial A, otherwise known as a dyadic, is formed from multiple vectors 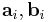$\mathbf{a}_i, \mathbf{b}_i$

$\mathbf{A} = \sum_i\mathbf{a}_i\mathbf{b}_i = \mathbf{a}_1\mathbf{b}_1%2B\mathbf{a}_2\mathbf{b}_2%2B\mathbf{a}_3\mathbf{b}_3%2B\cdots$

A dyadic which cannot be reduced to a sum of less than 3 dyads is said to be complete. In this case, the forming vectors are non-coplanar, see Chen (1983).

The following table classifies dyadics:

	Determinant	Adjoint	Matrix and its rank
Zero	= 0	= 0	= 0; rank 0: all zeroes
Linear	= 0	= 0	≠ 0; rank 1: at least one non-zero element and all 2x2 subdeterminants zero (single dyadic)
Planar	= 0	≠ 0 (single dyadic)	≠ 0; rank 2: at least one non-zero 2x2 subdeterminant
Complete	≠ 0	≠ 0	≠ 0; rank 3: non-zero determinant

Dyadics algebra

Dyadic with vector

There are 4 operations for a vector with a dyadic

$\begin{align} \mathbf{c}\cdot \mathbf{a} \mathbf{b}&=\left(\mathbf{c}\cdot\mathbf{a}\right)\mathbf{b}\\ \left(\mathbf{a}\mathbf{b}\right)\cdot \mathbf{c} &= \mathbf{a}\left(\mathbf{b}\cdot\mathbf{c}\right) \\ \mathbf{c} \times \left(\mathbf{ab}\right) &= \left(\mathbf{c}\times\mathbf{a}\right)\mathbf{b} \\ \left(\mathbf{ab}\right)\times\mathbf{c}&=\mathbf{a}\left(\mathbf{b}\times\mathbf{c}\right) \end{align}$

Dyadic with dyadic

There are 5 operations for a dyadic to another dyadic:

Simple-dot product

$\left(\mathbf{ab}\right)\cdot\left(\mathbf{cd}\right) = \mathbf{a}\left(\mathbf{b}\cdot\mathbf{c}\right)\mathbf{d}=\left(\mathbf{b}\cdot\mathbf{c}\right)\mathbf{ad}$

For 2 general dyadics A and B:

$\mathbf{A}=\sum _i \mathbf{a}_i\mathbf{b}_i$

$\mathbf{B}=\sum _i \mathbf{c}_i\mathbf{d}_i$

$\mathbf{A}\cdot\mathbf{B}=\sum _{i,j}\left(\mathbf{a}_i\mathbf{b}_i\right)\cdot\left(\mathbf{c}_j\mathbf{d}_j\right) = \sum _{i,j}\left(\mathbf{b}_i\cdot\mathbf{c}_j\right)\mathbf{a}_i\mathbf{d}_j = \left(\mathbf{b}_1\cdot\mathbf{c}_1\right)\mathbf{a}_1\mathbf{d}_1%2B\left(\mathbf{b}_1\cdot\mathbf{c}_2\right)\mathbf{a}_1\mathbf{d}_2%2B\text{...}%2B\left(\mathbf{b}_2\cdot\mathbf{c}_1\right)\mathbf{a}_2\mathbf{d}_1%2B\left(\mathbf{b}_2\cdot\mathbf{c}_2\right)\mathbf{a}_2\mathbf{d}_2%2B\text{...}$

Double-dot product

There are two ways to define the double dot product. Many sources use a definition of the double dot product rooted in the matrix double-dot product,

$\mathbf{ab}\colon\mathbf{cd}=\left(\mathbf{a}\cdot\mathbf{d}\right)\left(\mathbf{b}\cdot\mathbf{c}\right)$

whereas other sources use a definition unique (usually referred to as the "colon product") to dyads:

$\left(\mathbf{ab}\right):\left(\mathbf{cd}\right) = \mathbf{c}\cdot\left(\mathbf{ab}\right)\cdot\mathbf{d} = \left(\mathbf{a}\cdot\mathbf{c}\right)\left(\mathbf{b}\cdot\mathbf{d}\right)$

One must be careful when deciding which convention to use. As there are no analogous matrix operations for the remaining dyadic products, no ambiguities in their definitions appear.

The double-dot product is commutative.

$\mathbf{A} \colon \! \mathbf{B} = \mathbf{B} \colon \! \mathbf{A}$

There is a special double dot product with a transpose

$\mathbf{A} \colon \! \mathbf{B}^\mathrm{T} = \mathbf{A}^\mathrm{T} \colon \! \mathbf{B}$

Another identity is:

$\mathbf{A}\colon\mathbf{B}=\left(\mathbf{A}\cdot\mathbf{B}^\mathrm{T}\right)\colon \mathbf{I} =\left(\mathbf{B}\cdot\mathbf{A}^\mathrm{T}\right)\colon \mathbf{I}$

Dot–cross product

$\left(\mathbf{ab}\right) \!\!\!\begin{array}{c} _\cdot \\ ^\times \end{array}\!\!\! \left(\mathbf{c}\mathbf{d}\right)=\left(\mathbf{a}\cdot\mathbf{c}\right)\left(\mathbf{b}\times\mathbf{d}\right)$

Cross–dot product

$\left(\mathbf{ab}\right) \!\!\!\begin{array}{c} _\times \\ ^\cdot \end{array}\!\!\! \left(\mathbf{cd}\right)=\left(\mathbf{a}\times\mathbf{c}\right)\left(\mathbf{b}\cdot\mathbf{d}\right)$

Double-cross product

$\left(\mathbf{ab}\right) \!\!\!\begin{array}{c} _\times \\ ^\times \end{array}\!\!\! \left(\mathbf{cd}\right)=\left(\mathbf{a}\times\mathbf{c}\right)\left(\mathbf{b}\times \mathbf{d}\right)$

We can see that, for any dyad formed from two vectors a and b, its double cross product is zero.

$\left(\mathbf{ab}\right) \!\!\!\begin{array}{c} _\times \\ ^\times \end{array}\!\!\! \left(\mathbf{ab}\right)=\left(\mathbf{a}\times\mathbf{a}\right)\left(\mathbf{b}\times\mathbf{b}\right)= 0$

However, for 2 general dyadics, their double-cross product is defined as:

$\mathbf{A} \!\!\!\begin{array}{c} _\times \\ ^\times \end{array}\!\!\! \mathbf{B}=\sum _{i,j} \left(\mathbf{a}_i\times \mathbf{c}_j\right)\left(\mathbf{b}_i\times \mathbf{d}_j\right)$

For a dyadic double-cross product on itself, the result will generally be non-zero. For example, a dyadic A composed of six different vectors

$\mathbf{A}=\sum _{i=1}^3 \mathbf{a}_i\mathbf{b}_i$

has a non-zero self-double-cross product of

$\mathbf{A} \!\!\!\begin{array}{c} _\times \\ ^\times \end{array}\!\!\! \mathbf{A} = 2 \left[\left(\mathbf{a}_1\times \mathbf{a}_2\right)\left(\mathbf{b}_1\times \mathbf{b}_2\right)%2B\left(\mathbf{a}_2\times \mathbf{a}_3\right)\left(\mathbf{b}_2\times \mathbf{b}_3\right)%2B\left(\mathbf{a}_3\times \mathbf{a}_1\right)\left(\mathbf{b}_3\times \mathbf{b}_1\right)\right]$

Unit dyadic

For any vector a, there exist a unit dyadic I, such that

$\mathbf{I}\cdot\mathbf{a}=\mathbf{a}\cdot\mathbf{I}= \mathbf{a}$

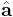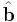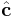For any base of 3 vectors a, b and c, with reciprocal base $\hat{{\mathbf{a}}}$ , $\hat{\mathbf{b}}$ and $\hat{\mathbf{c}}$ , the unit dyadic is defined by

$\mathbf{I} = \mathbf{a}\hat{\mathbf{a}} %2B \mathbf{b}\hat{\mathbf{b}} %2B \mathbf{c}\hat{\mathbf{c}}$

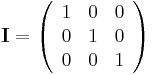
In Cartesian coordinates,

$\mathbf{I} = \hat{\mathbf{x}}\hat{\mathbf{x}} %2B \hat{{\mathbf{y}}}\hat{\mathbf{y}} %2B \hat{{\mathbf{z}}}\hat{\mathbf{z}}$

For an orthonormal base $\mathbf{x_i}=\mathbf{x_i'}$ ,

$\mathbf{I}=\sum _i \mathbf{x_i}\mathbf{x_i}$

The corresponding matrix is

$\mathbf{I}=\left( \begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ \end{array} \right)$

Rotation dyadic

For any vector a,

$\mathbf{a}\times \mathbf{I}$

is a 90 degree right hand rotation dyadic around a.

Some operations with unit dyadics

$\left(\mathbf{a}\times\mathbf{I}\right)\cdot\left(\mathbf{b}\times\mathbf{I}\right)= \mathbf{ab}-\left(\mathbf{a}\cdot\mathbf{b}\right)\mathbf{I}$

$\mathbf{I} \!\!\begin{array}{c} _\times \\ ^\cdot \end{array}\!\!\! \left(\mathbf{ab}\right)=\mathbf{b}\times\mathbf{a}$

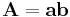
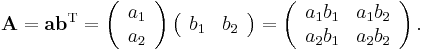
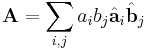
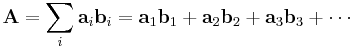
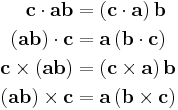
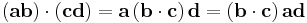
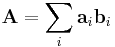
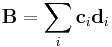
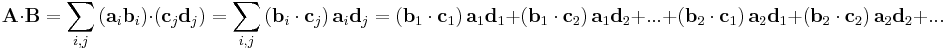
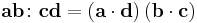
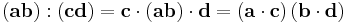
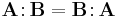
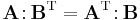
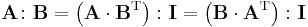
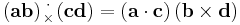
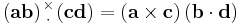
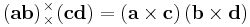
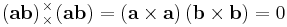
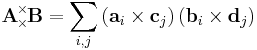
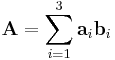
$\mathbf{I} \!\!\begin{array}{c} _\times \\ ^\times \end{array}\!\! \mathbf{A}=\left(\mathbf{A} \!\!\begin{array}{c} _\times \\ ^\times \end{array}\!\! \mathbf{I}\right)\mathbf{I}-\mathbf{A}^\mathrm{T}$

$\mathbf{I}\;\colon\left(\mathbf{ab}\right) = \left(\mathbf{I}\cdot\mathbf{a}\right)\cdot\mathbf{b} = \mathbf{a}\cdot\mathbf{b} = \text{Trace}\left(\mathbf{ab}\right)$

References

ISMO V. Lindell (1992). Methods for Electromagnetic Field Analysis. ISBN 019856239. .
Hollis C. Chen (1983). Theory of Electromagnetic Wave - A Coordinate-free approach. ISBN 0070106886. .