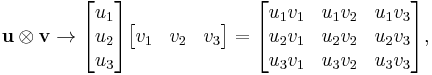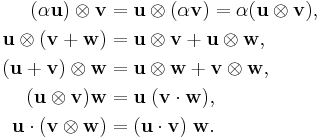Dyadic product

In mathematics, in particular multilinear algebra, the dyadic product

$\mathbb{P} = \mathbf{u}\otimes\mathbf{v}$

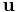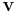of two vectors, $\mathbf{u}$ and $\mathbf{v}$ , each having the same dimension, is the tensor product of the vectors and results in a tensor of order two and rank one. It is also called outer product.

1 Components
2 Matrix representation
3 Identities
4 See also
5 Notes
6 References

Components

With respect to a chosen basis 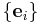$\{\mathbf{e}_i\}$ , the components 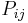$P_{ij}$ of the dyadic product 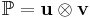$\mathbb{P} = \mathbf{u} \otimes \mathbf{v}$ may be defined by

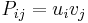$\displaystyle P_{ij} = u_i v_j$ ,

where

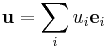$\mathbf{u} = \sum_i u_i \mathbf{e}_i$ ,

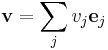$\mathbf{v} = \sum_j v_j \mathbf{e}_j$ ,

and

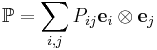$\mathbb{P} = \sum_{i,j} P_{ij} \mathbf{e}_i \otimes \mathbf{e}_j$ .

Matrix representation

The dyadic product can be simply represented as the square matrix obtained by multiplying 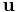$\mathbf{u}$ as a column vector by 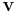$\mathbf{v}$ as a row vector. For example,

$\mathbf{u} \otimes \mathbf{v} \rightarrow \begin{bmatrix} u_1 \\ u_2 \\ u_3 \end{bmatrix} \begin{bmatrix} v_1 & v_2 & v_3 \end{bmatrix} = \begin{bmatrix} u_1v_1 & u_1v_2 & u_1v_3 \\ u_2v_1 & u_2v_2 & u_2v_3 \\ u_3v_1 & u_3v_2 & u_3v_3 \end{bmatrix} ,$

where the arrow indicates that this is only one particular representation of the dyadic product, referring to a particular basis. In this representation, the dyadic product is a special case of the Kronecker product.

Identities

The following identities are a direct consequence of the definition of the dyadic product^[1]:

$\begin{align} (\alpha \mathbf{u}) \otimes \mathbf{v} &= \mathbf{u} \otimes (\alpha \mathbf{v}) = \alpha (\mathbf{u} \otimes \mathbf{v}), \\ \mathbf{u} \otimes (\mathbf{v} %2B \mathbf{w}) &= \mathbf{u} \otimes \mathbf{v} %2B \mathbf{u} \otimes \mathbf{w}, \\ (\mathbf{u} %2B \mathbf{v}) \otimes \mathbf{w} &= \mathbf{u} \otimes \mathbf{w} %2B \mathbf{v} \otimes \mathbf{w}, \\ (\mathbf{u} \otimes \mathbf{v}) \mathbf{w} &= \mathbf{u}\; (\mathbf{v} \cdot \mathbf{w}), \\ \mathbf{u} \cdot (\mathbf{v} \otimes \mathbf{w}) &= (\mathbf{u} \cdot \mathbf{v})\; \mathbf{w}. \end{align}$

Notes

^ See Spencer (1992), page 19.

References

A.J.M. Spencer (1992). Continuum Mechanics. Dover Publications. ISBN 0486435946. .