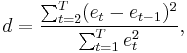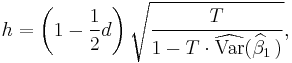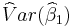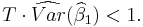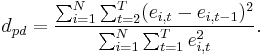Durbin–Watson statistic

In statistics, the Durbin–Watson statistic is a test statistic used to detect the presence of autocorrelation (a relationship between values separated from each other by a given time lag) in the residuals (prediction errors) from a regression analysis. It is named after James Durbin and Geoffrey Watson. However, the small sample distribution of this ratio was derived in a path-breaking article by John von Neumann (von Neumann, 1941). Durbin and Watson (1950, 1951) applied this statistic to the residuals from least squares regressions, and developed bounds tests for the null hypothesis that the errors are serially independent (not autocorrelated) against the alternative that they follow a first order autoregressive process. Later, John Denis Sargan and Alok Bhargava developed several von Neumann–Durbin–Watson type test statistics for the null hypothesis that the errors on a regression model follow a process with a unit root against the alternative hypothesis that the errors follow a stationary first order autoregression (Sargan and Bhargava, 1983).

Contents 1 Computing and interpreting the Durbin–Watson statistic 2 Durbin h-statistic 3 Durbin–Watson test for panel data 4 Implementations in statistics packages 5 See also 6 Notes 7 References 8 External links

Computing and interpreting the Durbin–Watson statistic

If e_t is the residual associated with the observation at time t, then the test statistic is

where T is the number of observations. Since d is approximately equal to 2(1 − r), where r is the sample autocorrelation of the residuals,^[1] d = 2 indicates no autocorrelation. The value of d always lies between 0 and 4. If the Durbin–Watson statistic is substantially less than 2, there is evidence of positive serial correlation. As a rough rule of thumb, if Durbin–Watson is less than 1.0, there may be cause for alarm. Small values of d indicate successive error terms are, on average, close in value to one another, or positively correlated. If d > 2 successive error terms are, on average, much different in value to one another, i.e., negatively correlated. In regressions, this can imply an underestimation of the level of statistical significance.

To test for positive autocorrelation at significance α, the test statistic d is compared to lower and upper critical values (d_L,α and d_U,α):

• If d < d_L,α, there is statistical evidence that the error terms are positively autocorrelated.
• If d > d_U,α, there is statistical evidence that the error terms are not positively autocorrelated.
• If d_L,α < d < d_U,α, the test is inconclusive.

Positive serial correlation is serial correlation in which a positive error for one observation increases the chances of a positive error for another observation.

Although positive serial correlation does not affect the consistency of the estimated regression coefficients, it does affect our ability to conduct valid statistical tests. First, the F-statistic to test for overall significance of the regression may be inflated because the mean squared error (MSE) will tend to underestimate the population error variance. Second, positive serial correlation typically causes the ordinary least squares (OLS) standard errors for the regression coefficients to underestimate the true standard errors. As a consequence, if positive serial correlation is present in the regression, standard linear regression analysis will typically lead us to compute artificially small standard errors for the regression coefficient. These small standard errors will cause the estimated t-statistic to be inflated, suggesting significance where perhaps there is none. The inflated t-statistic, may in turn, lead us to incorrectly reject null hypotheses, about population values of the parameters of the regression model more often than we would if the standard errors were correctly estimated. This Type I error could lead to improper investment recommendations.

To test for negative autocorrelation at significance α, the test statistic (4 − d) is compared to lower and upper critical values (d_L,α and d_U,α):

• If (4 − d) < d_L,α, there is statistical evidence that the error terms are negatively autocorrelated.
• If (4 − d) > d_U,α, there is statistical evidence that the error terms are not negatively autocorrelated.
• If d_L,α < (4 − d) < d_U,α, the test is inconclusive.

Negative serial correlation implies that a positive error for one observation increases the chance of a negative error for another observation and a negative error for one observation increases the chances of a positive error for another.

The critical values, d_L,α and d_U,α, vary by level of significance (α), the number of observations, and the number of predictors in the regression equation. Their derivation is complex—statisticians typically obtain them from the appendices of statistical texts.

An important note is that the Durbin–Watson statistic, while displayed by many regression analysis programs, is not relevant in many situations. For instance, if the error distribution is not normal, if there is higher-order autocorrelation, or if the dependent variable is in a lagged form as an independent variable, this is not an appropriate test for autocorrelation. A suggested test that does not have these limitations is the Breusch–Godfrey (serial correlation LM) Test.

Durbin h-statistic

The Durbin–Watson statistic is biased for autoregressive moving average models, so that autocorrelation is underestimated. But for large samples one can easily compute the unbiased normally distributed h-statistic:

using the Durbin–Watson statistic d and the estimated variance

of the regression coefficient of the lagged dependent variable, provided

Durbin–Watson test for panel data

For panel data this statistic was generalized as follows by Alok Bhargava et al. (1982):

If e_{i, t} is the residual from an OLS regression with fixed effects for each panel i, associated with the observation in panel i at time t, then the test statistic is

This statistic can be compared with tabulated rejection values [see Alok Bhargava et al. (1982), page 537]. These values are calculated dependent on T (length of the balanced panel—time periods the individuals were surveyed), K (number of regressors) and N (number of individuals in the panel). This test statistic can also be used for testing the null hypothesis of a unit root against stationary alternatives in fixed effects models using another set of bounds (Tables V and VI) tabulated by Alok Bhargava et al. (1982).

Implementations in statistics packages

1. R: the dwtest function in the lmtest package, and durbin.watson function in the car package.
2. MATLAB: the dwtest function in the Statistics Toolbox.
3. Mathematica: the Durbin–Watson (d) statistic is included as an option in the LinearModelFit function.
4. SAS: Is a standard output when using proc model and is an option (dw) when using proc reg.
5. Stata: the command -estat dwatson-, following -regress- in times series data. Engle's LM test for autoregressive conditional heteroskedasticity (ARCH), a test for time-dependent volatility, the Breusch–Godfrey test, and Durbin's alternative test for serial correlation are also available. All (except -dwatson-) tests separately for higher-order serial correlations. The Breusch–Godfrey test and Durbin's alternative test also allow regressors that are not strictly exogenous.
6. EXCEL: although Microsoft Excel 2007 does not have a specific Durbin–Watson function, the d-statistic may be calculated using "=SUMXMY2(x_array,y_array)/SUMSQ(array)"
7. Minitab: the option to report the statistic in the Session window can be found under the "Options" box under Regression and via the "Results" box under General Regression.

See also

• Time-series regression
• ACF / PACF

Notes

1. ^ Gujarati (2003) p. 469

References

External links

• Table for high n and k