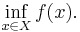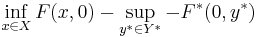Duality gap

In optimization problems in applied mathematics, the duality gap is the difference between the primal and dual solutions. If 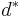$d^*$ is the optimal dual value and 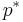$p^*$ is the optimal primal value then the duality gap is equal to 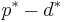$p^* - d^*$ . This value is always greater than or equal to 0. The duality gap is zero if and only if strong duality holds. Otherwise the gap is strictly positive and weak duality holds.^[1]

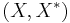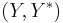In general given two dual pairs separated locally convex spaces $\left(X,X^*\right)$ and $\left(Y,Y^*\right)$ . Then given the function 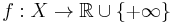$f: X \to \mathbb{R} \cup \{%2B\infty\}$ , we can define the primal problem by

$\inf_{x \in X} f(x). \,$

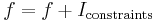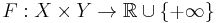If there are constraint conditions, these can be built in to the function $f$ by letting $f = f %2B I_{\mathrm{constraints}}$ where $I$ is the indicator function. Then let $F: X \times Y \to \mathbb{R} \cup \{%2B\infty\}$ be a perturbation function such that 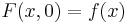$F(x,0) = f(x)$ . The duality gap is the difference given by

$\inf_{x \in X} F(x,0) - \sup_{y^* \in Y^*} -F^*(0,y^*)$

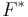where $F^*$ is the convex conjugate in both variables.^[2]^[3]^[4]

The duality gap is used in certain optimization methods to determine how far off from optimality the current solution is.^[5]

References

^ Borwein, Jonathan; Zhu, Qiji (2005). Techniques of Variational Analysis. Springer. ISBN 978-1441920263.
^ Radu Ioan Boţ; Gert Wanka; Sorin-Mihai Grad (2009). Duality in Vector Optimization. Springer. ISBN 9783642028854.
^ Ernö Robert Csetnek (2010). Overcoming the failure of the classical generalized interior-point regularity conditions in convex optimization. Applications of the duality theory to enlargements of maximal monotone operators. Logos Verlag Berlin GmbH. ISBN 9783832525033.
^ Zălinescu, C.. Convex analysis in general vector spaces. World Scientific Publishing Co., Inc. pp. 106–113. ISBN 981-238-067-1. MR 1921556.
^ Boyd, Stephen P.; Vandenberghe, Lieven (2004) (pdf). Convex Optimization. Cambridge University Press. ISBN 9780521833783. http://www.stanford.edu/~boyd/cvxbook/bv_cvxbook.pdf. Retrieved October 15, 2011.