Downsampling

In signal processing, downsampling (or "subsampling") is the process of reducing the sampling rate of a signal. This is usually done to reduce the data rate or the size of the data.

The downsampling factor (commonly denoted by M) is usually an integer or a rational fraction greater than unity. This factor multiplies the sampling time or, equivalently, divides the sampling rate. For example, if compact disc audio at 44,100 Hz is downsampled to 22,050 Hz before broadcasting over FM radio, the bit rate is reduced in half, from 1,411,200 bit/s to 705,600 bit/s, assuming that each sample retains its size of 16 bits. The audio was therefore downsampled by a factor of 2.

Contents

Maintaining the sampling theorem criterion

Since downsampling reduces the sampling rate, we must be careful to make sure the Shannon-Nyquist sampling theorem criterion is maintained. If the sampling theorem is not satisfied then the resulting digital signal will have aliasing. To ensure that the sampling theorem is satisfied, a low-pass filter is used as an anti-aliasing filter to reduce the bandwidth of the signal before the signal is downsampled; the overall process (low-pass filter, then downsample) is called decimation.

Note that the anti-aliasing filter must be a low-pass filter in downsampling. This is different from sampling a continuous signal, where either a low-pass filter or a band-pass filter may be used.

Remark: A bandpass signal, i.e. a band-limited signal whose minimum frequency is different from zero, can be downsampled avoiding superposition of the spectra if certain conditions are satisfied (see e.g. [1]).

Downsampling process

Consider a discrete signal 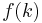f(k) on a radian frequency digital frequency range.

Downsampling by integer factor

Let M denote the downsampling factor.

  1. Filter the signal to ensure that the sampling theorem is satisfied. This filter should, theoretically, be the sinc filter with frequency cutoff at 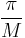\frac{\pi}{M}. Let the filtered signal be denoted g(k).
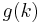  2. Reduce the data by picking out every 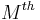M^{th} sample: 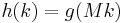h(k) = g(Mk). Data rate reduction occurs in this step.

The first step calls for the use of a perfect low-pass filter, which is not implementable for real-time signals. When choosing a realizable low-pass filter this will have to be considered along with the aliasing effects it will have. Realizable low-pass filters have a "skirt", where the response diminishes from near unity to near zero. So in practice the cutoff frequency is placed far enough below the theoretical cutoff that the filter's skirt is contained below the theoretical cutoff.

Downsampling by rational fraction

Let M/L denote the downsampling factor.

  1. Upsample by a factor of L
  2. Downsample by a factor of M

Note that a proper upsampling design requires an interpolation filter after increasing the data rate and that a proper downsampling design requires a filter before eliminating some samples. These two low-pass filters can be combined into a single filter.

Also note that these two steps are generally not reversible. Downsampling results in a loss of data and, if performed first, could result in data loss if there is any data filtered out by the downsampler's low-pass filter. Since both interpolation and anti-aliasing filters are low-pass filters, the filter with the smallest bandwidth is more restrictive and can therefore be used in place of both filters. When the rational fraction M/L is greater than unity then 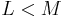L < M and the single low-pass filter should have cutoff at \pi/M.

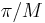See also

Theory
Sub-fields
Techniques
Sampling