Double-precision floating-point format

In computing, double precision is a computer number format that occupies two adjacent storage locations in computer memory. A double-precision number, sometimes simply called a double, may be defined to be an integer, fixed point, or floating point (in which case it is often referred to as FP64).

Modern computers with 32-bit storage locations use two memory locations to store a 64-bit double-precision number (a single storage location can hold a single-precision number). Double-precision floating-point is an IEEE 754 standard for encoding binary or decimal floating-point numbers in 64 bits (8 bytes).

Floating-point precisions
IEEE 754: 16-bit: Half (binary16) 32-bit: Single (binary32), decimal32 64-bit: Double (binary64), decimal64 128-bit: Quadruple (binary128), decimal128 Other: Minifloat · Extended precision Arbitrary precision

1 IEEE 754 double-precision binary floating-point format: binary64
- 1.1 Exponent encoding
- 1.2 Double-precision examples
2 See also

IEEE 754 double-precision binary floating-point format: binary64

Double-precision binary floating-point is a commonly used format on PCs, due to its wider range over single-precision floating point, even if it's at a performance and bandwidth cost. As with single-precision floating-point format, it lacks precision on integer numbers when compared with an integer format of the same size. It is commonly known simply as double. The IEEE 754 standard specifies a binary64 as having:

Sign bit: 1 bit
Exponent width: 11 bits
Significand precision: 53 bits (52 explicitly stored)

The format is written with the significand having an implicit integer bit of value 1, unless the written exponent is all zeros. With the 52 bits of the fraction significand appearing in the memory format, the total precision is therefore 53 bits (approximately 16 decimal digits, 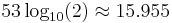$53\log_{10}(2) \approx 15.955$ ). The bits are laid out as follows:

The real value assumed by a given 64-bit double-precision data with a given biased exponent e and a 52-bit fraction is 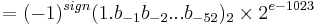$= (-1)^{sign}(1.b_{-1}b_{-2}...b_{-52})_2 \times 2^{e-1023}$ where more precisely we have :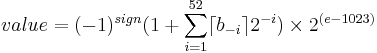 $value = (-1)^{sign}(1 %2B \sum_{i=1}^{52} \lceil b_{-i} \rceil 2^{-i} )\times 2^{(e-1023)}$

Between 2⁵²=4,503,599,627,370,496 and 2⁵³=9,007,199,254,740,992 the representable numbers are exactly the integers. For the next range, from 2⁵³ to 2⁵⁴, everything is multiplied by 2, so the representable numbers are the even ones, etc. Conversely, for the previous range from 2⁵¹ to 2⁵², the spacing is 0.5, etc.

The spacing as a fraction of the numbers in the range from 2ⁿ to 2ⁿ⁺¹ is 2ⁿ⁻⁵². The maximum relative rounding error when rounding a number to the nearest representable one (the machine epsilon) is therefore 2⁻⁵³.

Exponent encoding

The double-precision binary floating-point exponent is encoded using an offset-binary representation, with the zero offset being 1023; also known as exponent bias in the IEEE 754 standard. Examples of such representations would be:

E_min (1) = −1022
E (50) = −973
E_max (2046) = 1023

Thus, as defined by the offset-binary representation, in order to get the true exponent the exponent bias of 1023 has to be subtracted from the written exponent.

The exponents 0x000 and 0x7ff have a special meaning:

0x000 is used to represent zero (if F=0) and subnormals (if F≠0); and
0x7ff is used to represent infinity (if F=0) and NaNs (if F≠0),

where F is the fraction mantissa. All bit patterns are valid encoding.

Here, 0x is used as the prefix for numeric constants represented in Hexadecimal according to C notation.

Except for the above exceptions, the entire double-precision number is described by:

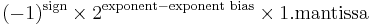
$(-1)^{\text{sign}} \times 2^{\text{exponent} - \text{exponent bias}} \times 1.\text{mantissa}$

Double-precision examples

0x 3ff0 0000 0000 0000   = 1
0x 3ff0 0000 0000 0001   ≈ 1.0000000000000002, the next higher number > 1
0x 3ff0 0000 0000 0002   ≈ 1.0000000000000004
0x 4000 0000 0000 0000   = 2
0x c000 0000 0000 0000   = –2

0x 0000 0000 0000 0001   = 2^-1022-52 ≈ 4.9406564584124654 x 10⁻³²⁴ (Min subnormal positive double)
0x 000f ffff ffff ffff   = 2^-1022 - 2^-1022-52 ≈ 2.2250738585072009 x 10^-308 (Max subnormal positive double)
0x 0010 0000 0000 0000   = 2^-1022 ≈ 2.2250738585072014 x 10⁻³⁰⁸ (Min normal positive double)
0x 7fef ffff ffff ffff   = (1 + (1 - 2^-52)) x 2¹⁰²³ ≈ 1.7976931348623157 x 10³⁰⁸ (Max Double)

0x 0000 0000 0000 0000   = 0
0x 8000 0000 0000 0000   = –0

0x 7ff0 0000 0000 0000   = Infinity
0x fff0 0000 0000 0000   = −Infinity

0x 3fd5 5555 5555 5555   ≈ 1/3

(1/3 rounds down instead of up like single precision, because of the odd number of bits in the significand.)

In more detail:

Given the hexadecimal representation 0x3fd5 5555 5555 5555,
  Sign = 0x0
  Exponent = 0x3fd = 1021
  Exponent Bias = 1023 (above)
  Mantissa = 0x5 5555 5555 5555
  Value = 2^{(Exponent − Exponent Bias)} × 1.Mantissa – Note the Mantissa must not be converted to decimal here
        = 2^–2 × (0x15 5555 5555 5555 × 2^–52)
        = 2^–54 × 0x15 5555 5555 5555
        = 0.333333333333333314829616256247390992939472198486328125
        ≈ 1/3

Double-precision floating-point format

Contents

IEEE 754 double-precision binary floating-point format: binary64

Exponent encoding

Double-precision examples

See also