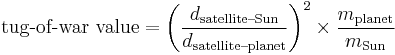Double planet
In astronomy, double planet and binary planet are informal terms used to describe a binary system of two astronomical objects that each satisfy the definition of planet and that are near enough to each other to have a significant gravitational effect on each other compared with the effect of the star(s) they orbit. As of 2010, there are no officially classified double planets in the Solar System. One unofficial definition is that the objects orbit a common center of gravity, the barycenter, that is above both their surfaces.
Similarly, there are also binary asteroids (also known as double minor planets) such as 90 Antiope, and binary Kuiper belt objects (KBOs) such as (79360) 1997 CS29 and 1998 WW31. The European Space Agency has referred to the Earth–Moon system as a type of double planet.[1] The IAU General Assembly in August 2006 considered a proposal that Pluto and Charon be reclassified as a double planet, but the proposal was abandoned.[2]
Contents |
Definition of a double planet
There has been some debate in the past on precisely where to draw the line between a double-planet and a planet–moon system. In most cases, this is not an issue because the satellite has a small mass relative to its host planet. In particular, with the exception of the Earth–Moon and Pluto–Charon systems, all satellites in the Solar System have masses less than 0.00025 (1⁄4000) the mass of the host planet or dwarf planet. On the other hand, the Moon to Earth mass ratio is 0.01230 (≈ 1⁄81), while the Charon to Pluto mass ratio is 0.117 (≈ 1⁄9).
A commonly accepted cutoff point by the vast majority of scientists for deciding between a planet–satellite or double-planet system is based on the location of the barycenter of the two objects (that is, the center of gravity). If the barycenter is not located under the surface of either body, then one may refer to the system as a double-planet system. In this case, both bodies orbit about a point in the free space between them. By this definition, Pluto and Charon would be seen as a double-dwarf-planet system, whereas the Earth and Moon would remain defined as a planet–satellite system. Due to the increasing distance from Earth of the Moon's orbital path (because of tidal forces, the Moon currently drifts away from Earth about 3.74 cm or 1.5 in per year[3]), the barycenter that now lies under the surface of the Earth will someday move outside the surface. So by this definition, the Earth–Moon system might be seen as a double planet billions of years from now.[3] In 2006 the International Astronomical Union briefly considered a formal definition of double planet which would have included Pluto and Charon, but this definition was not ratified.
If the definition of a double- or binary-star system is used as a comparison, and it depended only on the location of the barycenter, then any revolving body with a barycenter beneath a star's surface would be a planet, and any body with a barycenter lying outside the surface of the star would be another star. In the Solar System, all of the major planets would be planets under this definition except one. The Sun–Jupiter barycenter is the only center of mass that lies outside the surface of the Sun.[4] Therefore, since Jupiter is not a star, the difficulty faced by astronomers to derive a reality-based definition of double planet begins to become clear.
Tug-of-war definition
Isaac Asimov suggested a distinction between planet–moon and double-planet systems based in part on what he called a "tug-of-war" value.[4] This quantity is simply the relationships between the masses of the primary planet and the Sun combined with the squared distances between the satellite and its planet and the Sun:
where d is the distance between the satellite and the planet and, respectively, the Sun. This formula actually reflects the relation of the gravitational forces the satellite "feels" from the planet and from the Sun. The tug-of-war figure for Saturn's moon Titan is 380, which means that Saturn's hold on Titan is 380 times as strong as the Sun's hold on Titan (however, this figure does not reflect the orbital stability which is better estimated by the ratio of the satellite orbit to Hill sphere of the planet with respect to the Sun).
Asimov figured tug-of-war values for several satellites of all the planets that have them except for dwarf planet Pluto, because very little was known about Pluto and its satellite Charon at the time. He showed that even the great gas giant, Jupiter, had only a slightly better hold than the Sun on its outer, captured satellites, some with tug-of-war values not much higher than one. Yet in every case the tug-of-war value was found to be greater than one, so in every case the Sun "loses" the tug of war with the planets.
In the case of the Earth's Moon, the Sun actually "wins" the tug of war with a value of only 0.46, which means that Earth's hold on the Moon is less than half the Sun's hold. Since the Sun's gravitational effect on the Moon is more than twice that of Earth's, Asimov reasoned that the Earth and Moon must form a double-planet system. This was one of several arguments in Asimov's writings for considering the Moon to be a planet rather than a satellite.[4]
We might look upon the Moon, then, as neither a true satellite of the Earth nor a captured one, but as a planet in its own right, moving about the Sun in careful step with the Earth. To be sure, from within the Earth-Moon system, the simplest way of picturing the situation is to have the Moon revolve about the Earth; but if you were to draw a picture of the orbits of the Earth and Moon about the Sun exactly to scale, you would see that the Moon's orbit is everywhere concave toward the Sun. It is always "falling toward" the Sun. All the other satellites, without exception, "fall away" from the Sun through part of their orbits, caught as they are by the superior pull of their primary planets – but not the Moon.[4]— Isaac Asimov
See here for a more detailed explanation of this.
Double planets in fiction
- New Washington and Franklin (Jerry Pournelle's The Prince)
- Opal and Quake (Charles Sheffield's Summertide)
- Iscandar and Gamilus (Space Battleship Yamato)
- Roche and Eau (Robert L. Forward's Rocheworld)
- Urras and Anarres (Ursula K. Le Guin's The Dispossessed)
- Genji and Chujo (Murasaki)
- Caprica and Gemenon (Caprica & Battlestar Galactica)
- Fire and Water (Lexx)
- Anatoray and Disith, collectively called "Prester" (Last Exile)
- Clom and Raxacoricofallapatorius (Doctor Who)
- Talus and Tralus (Star Wars Expanded Universe)
See also
- 2006 definition of planet
- Definition of a planet
- Hill sphere
- Natural satellite
- Orbit of the Moon
- 3753 Cruithne
- Co-orbital configuration
Notes
- ^ a b "Welcome to the double planet". ESA. 2003-10-05. http://www.esa.int/esaMI/SMART-1/SEMO1VMKPZD_0.html. Retrieved 2009-11-12.
- ^ "The IAU draft definition of "planet" and "plutons"". International Astronomical Union. 2006-08-16. http://www.iau.org/public_press/news/release/iau0601/. Retrieved 2008-05-17.
- ^ a b Robert Roy Britt (2006-08-18). "Earth's moon could become a planet". CNN Science & Space. http://edition.cnn.com/2006/TECH/space/08/18/moon.planet. Retrieved 2009-11-25.
- ^ a b c d Asimov, Isaac (1975). "Just Mooning Around", collected in Of time and space, and other things. Avon.
References
- "Clyde Tombaugh (1906-97) Astronomer who discovered the Solar System's ninth planet", Nature 385 (1997) 778 (Pluto and Charon are "the only known example of a true double planet".)
- "It's not easy to make the Moon", Nature 389 (1997) 327 (comparing double planet theory of Moon formation and Pluto-Charon as double planet)
Further reading
- Detecting companions to extrasolar planets using mutual events, J. Cabrera, J. Schneider, 2007