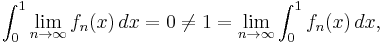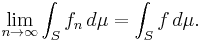Dominated convergence theorem
In measure theory, Lebesgue's dominated convergence theorem provides sufficient conditions under which two limit processes commute, namely Lebesgue integration and almost everywhere convergence of a sequence of functions. The dominated convergence theorem does not hold for the Riemann integral because the limit of a sequence of Riemann-integrable functions is in many cases not Riemann-integrable. Its power and utility are two of the primary theoretical advantages of Lebesgue integration over Riemann integration.
It is widely used in probability theory, since it gives a sufficient condition for the convergence of expected values of random variables.
Contents |
Statement of the theorem
Let {ƒn} denote a sequence of real-valued measurable functions on a measure space (S, Σ, μ). Assume that the sequence converges pointwise to a function ƒ and is dominated by some integrable function g in the sense that
for all numbers n in the index set of the sequence and all points x in S. Then the limiting function ƒ is integrable and
(By integrable we mean
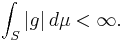 )
)
Remarks:
- The convergence of the sequence and domination by g can be relaxed to hold only μ-almost everywhere provided the measure space (S, Σ, μ) is complete or ƒ is chosen as a measurable function which agrees μ-almost everywhere with the μ-almost everywhere existing pointwise limit. (These precautions are necessary, because otherwise there might exist a non-measurable subset of a μ-null set N ∈ Σ, hence ƒ might not be measurable.)
- The condition that there is a dominating integrable function g can be relaxed to uniform integrability of the sequence {ƒn}, see Vitali convergence theorem.
Proof of the theorem
Lebesgue's dominated convergence theorem is a special case of the Fatou–Lebesgue theorem. Below is a direct proof, using Fatou’s lemma as the essential tool.
As the pointwise limit of the sequence, ƒ is also measurable and dominated by g, hence integrable. Furthermore,
for all n and
By the reverse Fatou lemma,
Using linearity and monotonicity of the Lebesgue integral,
and the theorem follows.
If the assumptions hold only μ-almost everywhere, then there exists a μ-null set N ∈ Σ such that the functions ƒn1N satisfy the assumptions everywhere on S. Then ƒ(x) is the pointwise limit of ƒn(x) for x ∈ S \ N and ƒ(x) = 0 for x ∈ N, hence ƒ is measurable. The values of the integrals are not influenced by this μ-null set N.
Discussion of the assumptions
The assumption that the sequence is dominated by some integrable g can not be dispensed with. This may be seen as follows: define ƒn(x) = n for x in the interval (0, 1/n] and ƒn(x) = 0 otherwise. Any g which dominates the sequence must also dominate the pointwise supremum h = supn ƒn. Observe that
by the divergence of the harmonic series. Hence, the monotonicity of the Lebesgue integral tells us that there exists no integrable function which dominates the sequence on [0,1]. A direct calculation shows that integration and pointwise limit do not commute for this sequence:
because the pointwise limit of the sequence is the zero function. Note that the sequence {ƒn} is not even uniformly integrable, hence also the Vitali convergence theorem is not applicable.
Bounded convergence theorem
One corollary to the dominated convergence theorem is the bounded convergence theorem, which states that if ƒ1, ƒ2, ƒ3, … is a sequence of uniformly bounded real-valued measurable functions which converges pointwise on a bounded measure space (S, Σ, μ) (i.e. one in which μ(S) is finite) to a function ƒ, then the limit ƒ is an integrable function and
Remark: The pointwise convergence and uniform boundedness of the sequence can be relaxed to hold only μ-almost everywhere, provided the measure space (S, Σ, μ) is complete or ƒ is chosen as a measurable function which agrees μ-almost everywhere with the μ-almost everywhere existing pointwise limit.
Proof
Since the sequence is uniformly bounded, there is a real number M such that |ƒn(x)| ≤ M for all x ∈ S and for all n. Define g(x) = M for all x ∈ S. Then the sequence is dominated by g. Furthermore, g is integrable since it is a constant function on a set of finite measure. Therefore the result follows from the dominated convergence theorem.
If the assumptions hold only μ-almost everywhere, then there exists a μ-null set N ∈ Σ such that the functions ƒn1N satisfy the assumptions everywhere on S.
Extensions
The dominated convergence theorem applies also to measurable functions with values in a Banach space, with the dominating function still being non-negative and integrable as above.
See also
- Convergence of random variables, Convergence in mean
- Monotone convergence theorem (does not require domination by an integrable function but assumes monotonicity of the sequence instead)
- Scheffé’s lemma
- Uniform integrability
- Vitali convergence theorem (a generalization of Lebesgue's dominated convergence theorem)
References
- Bartle, R.G. (1995). The elements of integration and Lebesgue measure. Wiley Interscience.
- Royden, H.L. (1988). Real analysis. Prentice Hall.
- Williams, D. (1991). Probability with martingales. Cambridge University Press. ISBN 0-521-40605-6.
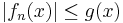
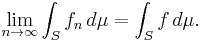
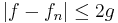
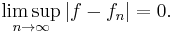
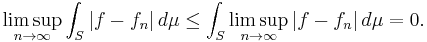
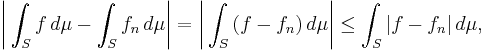
![\int_0^1 h(x)\,dx
\ge \int_{1/m}^1{h(x)\,dx}
= \sum_{n=1}^{m-1} \int_{\left(\frac1{n%2B1},\frac1n\right]}{n\,dx}
= \sum_{n=1}^{m-1} \frac{1}{n%2B1}
\to \infty \quad \text{as }m\to\infty](/2012-wikipedia_en_all_nopic_01_2012/I/2addf2eec53134138612631fc7b9b2a4.png)