Distributed constraint optimization
Distributed constraint optimization (DCOP or DisCOP) is the distributed analogue to constraint optimization. A DCOP is a problem in which a group of agents must distributedly choose values for a set of variables such that the cost of a set of constraints over the variables is either minimized or maximized.
Distributed Constraint Satisfaction is a framework for describing a problem in terms of constraints that are known and enforced by distinct participants (agents). The constraints are described on some variables with predefined domains, and have to be assigned to the same values by the different agents.
Problems defined with this framework can be solved by any of the algorithms that are proposed for it.
The framework was used under different names in the 1980s. The first known usage with the current name is in 1990.
Contents |
Definitions
DCOP
A DCOP can be defined as a tuple 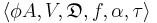 , where:
, where:
 is a set of agents;
is a set of agents; is a set of variables,
is a set of variables,  ;
;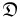 is a set of domains,
is a set of domains, 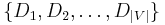 , where each
, where each 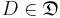 is a finite set containing the values to which its associated variable may be assigned;
is a finite set containing the values to which its associated variable may be assigned; is function[1][2]
is function[1][2]
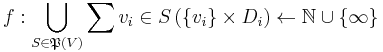
 is a function
is a function 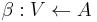 mapping variables to their associated agent.
mapping variables to their associated agent. 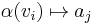 implies that it is agent
implies that it is agent 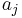 's responsibility to assign the value of variable
's responsibility to assign the value of variable 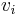 . Note that it is not necessarily true that
. Note that it is not necessarily true that  is either an injection or surjection; and
is either an injection or surjection; and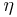 is an operator that aggregates all of the individual
is an operator that aggregates all of the individual  costs for all possible variable assignments. This is usually accomplished through summation:
costs for all possible variable assignments. This is usually accomplished through summation:
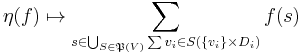 .
.
The objective of a DCOP is to have each agent assign values to its associated variables in order to either minimize or maximize 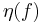 for a given assignment of the variables.
for a given assignment of the variables.
Context
A Context is a variable assignment for a DCOP. This can be thought of as a function mapping variables in the DCOP to their current values:
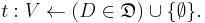
Note that a context is essentially a partial solution and need not contain values for every variable in the problem; therefore, 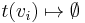 implies that the agent
implies that the agent 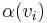 has not yet assigned a value to variable
has not yet assigned a value to variable 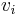 . Given this representation, the "domain" (i.e., the set of input values) of the function
. Given this representation, the "domain" (i.e., the set of input values) of the function f can be thought of as the set of all possible contexts for the DCOP. Therefore, in the remainder of this article we may use the notion of a context (i.e., the  function) as an input to the
function) as an input to the  function.
function.
Example problems
Distributed graph coloring
The graph coloring problem is as follows: given a graph 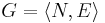 and a set of colors
and a set of colors  , assign each vertex,
, assign each vertex, 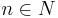 , a color,
, a color, 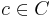 , such that the number of adjacent vertices with the same color is minimized.
, such that the number of adjacent vertices with the same color is minimized.
As a DCOP, there is one agent per vertex that is assigned to decide the associated color. Each agent has a single variable whose associated domain is of cardinality 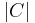 (there is one domain value for each possible color). For each vertex
(there is one domain value for each possible color). For each vertex 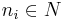 , create a variable in the DCOP
, create a variable in the DCOP 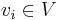 with domain
with domain 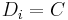 . For each pair of adjacent vertices
. For each pair of adjacent vertices 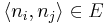 , create a constraint of cost 1 if both of the associated variables are assigned the same color:
, create a constraint of cost 1 if both of the associated variables are assigned the same color:
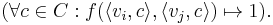
The objective, then, is to minimize 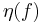 .
.
Distributed multiple knapsack problem
The distributed multiple- variant of the knapsack problem is as follows: given a set of items of varying volume and a set of knapsacks of varying capacity, assign each item to a knapsack such that the amount of overflow is minimized. Let  be the set of items,
be the set of items,  be the set of knapsacks,
be the set of knapsacks, 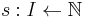 be a function mapping items to their volume, and
be a function mapping items to their volume, and 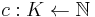 be a function mapping knapsacks to their capacities.
be a function mapping knapsacks to their capacities.
To encode this problem as a DCOP, for each 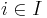 create one variable
create one variable 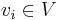 with associated domain
with associated domain 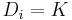 . Then for all possible context
. Then for all possible context  :
:
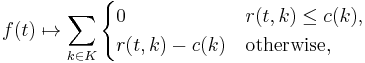
where 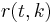 is a function such that
is a function such that
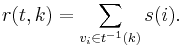
Algorithms
DCOP algorithms can be classified according to the search strategy (best-first search or depth-first branch-and-bound search), the synchronization among agents (synchronous or asynchronous), the communication among agents (point-to-point with neighbors in the constraint graph or broadcast) and the main communication topology (chain or tree).[3] ADOPT, for example, uses best-first search, asynchronous synchronization, point-to-point communication between neighboring agents in the constraint graph and a constraint tree as main communication topology.
| Algorithm Name | Year Introduced | Memory Complexity | Number of Messages | Correctness/ Completeness |
Implementations |
|---|---|---|---|---|---|
| NCBB No-Commitment Branch and Bound[4] |
2006 | Polynomial (or any-space[5]) | Exponential | Proven | Reference Implementation: not publicly released |
| DPOP Distributed Pseudotree Optimization Procedure[6] |
2005 | Exponential | Linear | Proven | Reference Implementation: FRODO (GNU Affero GPL) |
| OptAPO Asynchronous Partial Overlay[7] |
2004 | Polynomial | Exponential | Proven, but proof of completeness has been challenged[8] | Reference Implementation: OptAPO |
| Adopt Asynchronous Backtracking[9] |
2003 | Polynomial (or any-space[10]) | Exponential | Proven | Reference Implementation: Adopt |
| Secure Multiparty Computation For Solving DisCSPs (MPC-DisCSP1-MPC-DisCSP4) |
2003 | Note: secure if 1/2 of the participants are trustworthy | |||
| Secure Computation with Semi-Trusted Servers | 2002 | Note: security increases with the number of trustworthy servers | |||
| ABTR Asynchronous Backtracking with Reordering |
2001 | Note: eordering in ABT with bounded nogoods | |||
| DMAC Maintaining Asynchronously Consistencies |
2001 | Note: the fastest algorithm | |||
| AAS Asynchronous Aggregation Search |
2000 | aggregation of values in ABT | |||
| DFC Distributed Forward Chaining |
2000 | Note: low, comparable to ABT | |||
| DBA Distributed Breakout Algorithm |
1995 | Note: incomplete but fast | FRODO version 1 | ||
| AWC Asynchronous Weak-Commitment |
1994 | Note: reordering, fast, complete (only with exponential space) | |||
| ABT Asynchronous Backtracking |
1992 | Note: static ordering, complete |
Hybrids of these DCOP algorithms also exist. BnB-Adopt[3], for example, changes the search strategy of Adopt from best-first search to depth-first branch-and-bound search.
See also
Notes and references
- ^ "
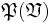 " denotes the power set of
" denotes the power set of 
- ^ "
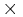 " and "
" and "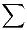 " denote the Cartesian product.
" denote the Cartesian product. - ^ a b Yeoh, William; Felner, Ariel; Koenig, Sven (2008), "BnB-ADOPT: An Asynchronous Branch-and-Bound DCOP Algorithm", Proceedings of the Seventh International Joint Conference on Autonomous Agents and Multiagent Systems, pp. 591–598, http://idm-lab.org/bib/abstracts/Koen08d.html
- ^ Chechetka, Anton; Sycara, Katia (May 2006), "No-Commitment Branch and Bound Search for Distributed Constraint Optimization", Proceedings of the Fifth International Joint Conference on Autonomous Agents and Multiagent Systems, pp. 1427–1429, http://www.ri.cmu.edu/pub_files/pub4/chechetka_anton_2006_2/chechetka_anton_2006_2.pdf
- ^ Chechetka, Anton; Sycara, Katia (March 2006), "An Any-space Algorithm for Distributed Constraint Optimization", Proceedings of the AAAI Spring Symposium on Distributed Plan and Schedule Management, http://www.ri.cmu.edu/pub_files/pub4/chechetka_anton_2006_1/chechetka_anton_2006_1.pdf
- ^ Petcu, Adrian; Faltings, Boi (August 2005), "DPOP: A Scalable Method for Multiagent Constraint Optimization", Proceedings of the 19th International Joint Conference on Artificial Intelligence, IJCAI 2005, Edinburgh, Scotland, pp. 266-271, http://liawww.epfl.ch/cgi-bin/Pubs/single_entry?bibtex_key=Petcu2005
- ^ Mailler, Roger; Lesser, Victor (2004), "Solving Distributed Constraint Optimization Problems Using Cooperative Mediation", Proceedings of the Third International Joint Conference on Autonomous Agents and Multiagent Systems, IEEE Computer Society, pp. 438–445, ftp://mas.cs.umass.edu/pub/mailler/mailler-569.pdf
- ^ Grinshpoun, Tal; Zazon, Moshe; Binshtok, Maxim; Meisels, Amnon (2007), "Termination Problem of the APO Algorithm", Proceedings of the Eighth International Workshop on Distributed Constraint Reasoning, pp. 117–124, http://liawww.epfl.ch/Publications/Archive/DCR07Proceedings.pdf
- ^ The originally published version of Adopt was uninformed, see Modi, Pragnesh Jay; Shen, Wei-Min; Tambe, Milind; Yokoo, Makoto (2003), "An asynchronous complete method for distributed constraint optimization", Proceedings of the second international joint conference on autonomous agents and multiagent systems, ACM Press, pp. 161–168, http://teamcore.usc.edu/papers/2003/modi-aamas03.pdf. The original version of Adopt was later extended to be informed, that is, to use estimates of the solution costs to focus its search and run faster, see Ali, Syed; Koenig, Sven; Tambe, Milind (2005), "Preprocessing Techniques for Accelerating the DCOP Algorithm ADOPT", Proceedings of the fourth international joint conference on autonomous agents and multiagent systems, ACM Press, pp. 1041–1048, http://teamcore.usc.edu/papers/2005/aamas-paper.pdf. This extension of Adopt is typically used as reference implementation of Adopt.
- ^ Matsui, Toshihiro; Matsuo, Hiroshi; Iwata, Akira (February), "Efficient Method for Asynchronous Distributed Constraint Optimization Algorithm", Proceedings of Artificial Intelligence and Applications, pp. 727–732, http://www.matlab.nitech.ac.jp/~matsuo/AIA05-1.pdf
Books and Surveys
- Faltings, Boi (2006), "Distributed Constraint Programming", in Walsh, Toby, Handbook of Constraint Programming, Elsevier, ISBN 978-0-444-52726-4, http://www.elsevier.com/wps/find/bookdescription.cws_home/708863/description A chapter in an edited book.
- Shoham, Yoav; Leyton-Brown, Kevin (2009), Multiagent Systems: Algorithmic, Game-Theoretic, and Logical Foundations, New York: Cambridge University Press, ISBN 978-0-521-89943-7, http://www.masfoundations.org See Chapters 1 and 2; downloadable free online.
- Yokoo, Makoto (2001), Distributed constraint satisfaction: Foundations of cooperation in multi-agent systems, Springer, ISBN 978-3-540-67596-9
- Yokoo, M., and Hirayama, K. (2000). Algorithms for distributed constraint satisfaction: A review. Proceedings of the International Joint Conference on Autonomous Agents and Multiagent Systems (pp. 185–207). A survey.