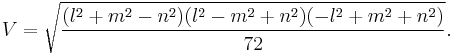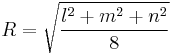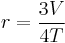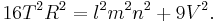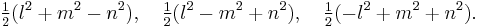Disphenoid

A disphenoid is a tetrahedron whose four faces are identical acute-angled triangles.^[1] It can also be described as a tetrahedron with opposite equal edges. Other names are isosceles tetrahedron and equifacial tetrahedron. All the solid angles and vertex figures of a disphenoid are the same. However, a disphenoid is not a regular polyhedron, because its faces are not regular polygons. The centers in the circumscribed and inscribed spheres coincide with the centroid of the disphenoid.^[2]

1 Special cases
2 Metric formulas
3 Honeycombs and crystals
4 See also
5 References
6 External links

Special cases

The faces of a tetragonal disphenoid are isosceles; the faces of a rhombic disphenoid are scalene. If the faces are equilateral triangles, one obtains a regular tetrahedron, which is not normally considered a disphenoid.

Metric formulas

The volume of a disphenoid with opposite edges of length l, m and n is given by^[2]

$V=\sqrt{\frac{(l^2%2Bm^2-n^2)(l^2-m^2%2Bn^2)(-l^2%2Bm^2%2Bn^2)}{72}}.$

The circumscribed sphere has radius^[2]

$R=\sqrt{\frac{l^2%2Bm^2%2Bn^2}{8}}$

and the inscribed sphere has radius^[2]

$r=\frac{3V}{4T}$

where V is the volume of the disphenoid and T is the area of any face, which is given by Heron's formula. There is also the following interesting relation connecting the volume and the circumradius:^[2]

$\displaystyle 16T^2R^2=l^2m^2n^2%2B9V^2.$

The square of the lengths of the bimedians are^[2]

$\tfrac{1}{2}(l^2%2Bm^2-n^2),\quad \tfrac{1}{2}(l^2-m^2%2Bn^2),\quad \tfrac{1}{2}(-l^2%2Bm^2%2Bn^2).$

Honeycombs and crystals

Some tetragonal disphenoids will form honeycombs. The disphenoid whose four vertices are (-1, 0, 0), (1, 0, 0), (0, 1, 1), and (0, 1, -1) is such a disphenoid.^[3] Each of its four faces is an isosceles triangle with edges of lengths √3, √3, and 2. It can tesselate space to form the disphenoid tetrahedral honeycomb. As Gibb^[4] describes, it can be folded without cutting or overlaps from a single sheet of a4 paper.

"Disphenoid" is also used to describe two forms of crystal:

A wedge-shaped crystal form of the tetragonal or orthorhombic system. It has four triangular faces that are alike and that correspond in position to alternate faces of the tetragonal or orthorhombic dipyramid. It is symmetrical about each of three mutually perpendicular diad axes of symmetry in all classes except the tetragonal-disphenoidal, in which the form is generated by an inverse tetrad axis of symmetry.

A crystal form bounded by eight scalene triangles arranged in pairs, constituting a tetragonal scalenohedron.

References

^ *Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. p. 15
^ ^a ^b ^c ^d ^e ^f Leech, John (1950), "Some properties of the isosceles tetrahedron", Mathematical Gazette 34 (310): 269-271 .
^ Coxeter, pp. 71–72; Senechal, Marjorie (1981). "Which tetrahedra fill space?". Mathematics Magazine 54 (5): 227–243. doi:10.2307/2689983. JSTOR 2689983.
^ Gibb, William (1990). "Paper patterns: solid shapes from metric paper". Mathematics in School 19 (3): 2–4. Reprinted in Pritchard, Chris, ed. (2003). The Changing Shape of Geometry: Celebrating a Century of Geometry and Geometry Teaching. Cambridge University Press. pp. 363–366. ISBN 0-521-53162-4.

External links

Weisstein, Eric W., "Disphenoid" from MathWorld.