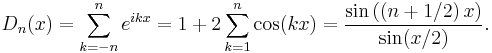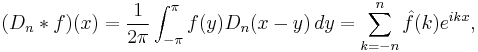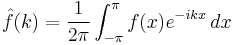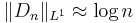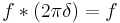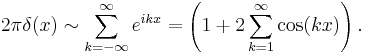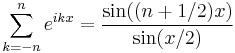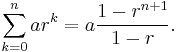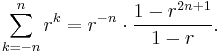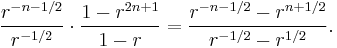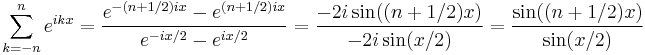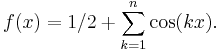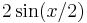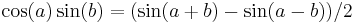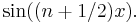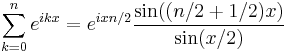Dirichlet kernel
In mathematical analysis, the Dirichlet kernel is the collection of functions
It is named after Johann Peter Gustav Lejeune Dirichlet.
The importance of the Dirichlet kernel comes from its relation to Fourier series. The convolution of Dn(x) with any function f of period 2π is the nth-degree Fourier series approximation to f, i.e., we have
where
is the kth Fourier coefficient of f. This implies that in order to study convergence of Fourier series it is enough to study properties of the Dirichlet kernel. Of particular importance is the fact that the L1 norm of Dn diverges to infinity as n → ∞. One can estimate that
where 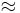 denotes "is of the order." This lack of uniform integrability is behind many divergence phenomena for the Fourier series. For example, together with the uniform boundedness principle, it can be used to show that the Fourier series of a continuous function may fail to converge pointwise, in rather dramatic fashion. See convergence of Fourier series for further details.
denotes "is of the order." This lack of uniform integrability is behind many divergence phenomena for the Fourier series. For example, together with the uniform boundedness principle, it can be used to show that the Fourier series of a continuous function may fail to converge pointwise, in rather dramatic fashion. See convergence of Fourier series for further details.
Contents |
Relation to the delta function
Take the periodic Dirac delta function, which is not really a function, in the sense of mapping one set into another, but is rather a "generalized function", also called a "distribution", and multiply by 2π. We get the identity element for convolution on functions of period 2π. In other words, we have
for every function f of period 2π. The Fourier series representation of this "function" is
Therefore the Dirichlet kernel, which is just the sequence of partial sums of this series, can be thought of as an approximate identity. Abstractly speaking it is not however an approximate identity of positive elements (hence the failures mentioned above).
Proof of the trigonometric identity
displayed at the top of this article may be established as follows. First recall that the sum of a finite geometric series is
In particular, we have
Multiply both the numerator and the denominator by r−1/2, getting
In the case r = eix we have
as required.
Alternative proof of the trigonometric identity
Start with the series
Multiply both sides of the above by
and use the trigonometric identity
to reduce the r.h.s. to
Variant of identity
If the sum is only over positive integers (which may arise when computing a DFT that is not centered), then using similar techniques we can show the following identity:
References
- Andrew M. Bruckner, Judith B. Bruckner, Brian S. Thomson: Real Analysis. ClassicalRealAnalysis.com 1996, ISBN 013458886X, S.620 (vollständige Online-Version (Google Books))
- Dirichlet-Kernel at PlanetMath