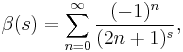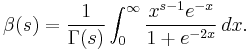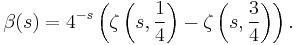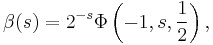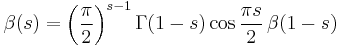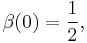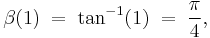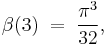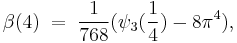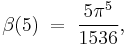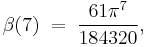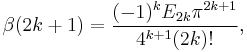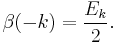Dirichlet beta function

In mathematics, the Dirichlet beta function (also known as the Catalan beta function) is a special function, closely related to the Riemann zeta function. It is a particular Dirichlet L-function, the L-function for the alternating character of period four.

Definition

The Dirichlet beta function is defined as

$\beta(s) = \sum_{n=0}^\infty \frac{(-1)^n} {(2n%2B1)^s},$

or, equivalently,

$\beta(s) = \frac{1}{\Gamma(s)}\int_0^{\infty}\frac{x^{s-1}e^{-x}}{1 %2B e^{-2x}}\,dx.$

In each case, it is assumed that Re(s) > 0.

Alternatively, the following definition, in terms of the Hurwitz zeta function, is valid in the whole complex s-plane:

$\beta(s) = 4^{-s} \left( \zeta\left(s,{1 \over 4}\right)-\zeta\left( s, {3 \over 4}\right) \right).$

Another equivalent definition, in terms of the Lerch transcendent, is:

$\beta(s) = 2^{-s} \Phi\left(-1,s,{{1} \over {2}}\right),$

which is once again valid for all complex values of s.

The functional equation extends the beta function to the left side of the complex plane Re(s)<0. It is given by

$\beta(s)=\left(\frac{\pi}{2}\right)^{s-1} \Gamma(1-s) \cos \frac{\pi s}{2}\,\beta(1-s)$

where Γ(s) is the gamma function.

Some special values include:

$\beta(0)= \frac{1}{2},$

$\beta(1)\;=\;\tan^{-1}(1)\;=\;\frac{\pi}{4},$

$\beta(2)\;=\;G,$

where G represents Catalan's constant, and

$\beta(3)\;=\;\frac{\pi^3}{32},$

$\beta(4)\;=\;\frac{1}{768}(\psi_3(\frac{1}{4})-8\pi^4),$

$\beta(5)\;=\;\frac{5\pi^5}{1536},$

$\beta(7)\;=\;\frac{61\pi^7}{184320},$

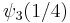where $\psi_3(1/4)$ in the above is an example of the polygamma function. More generally, for any positive integer k:

$\beta(2k%2B1)={{{({-1})^k}{E_{2k}}{\pi^{2k%2B1}} \over {4^{k%2B1}}(2k)!}},$

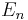where $\!\ E_{n}$ represent the Euler numbers. For integer k ≥ 0, this extends to:

$\beta(-k)={{E_{k}} \over {2}}.$

Hence, the function vanishes for all odd negative integral values of the argument.

J. Spanier and K. B. Oldham, An Atlas of Functions, (1987) Hemisphere, New York.
Weisstein, Eric W., "Dirichlet Beta Function" from MathWorld.