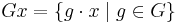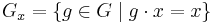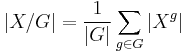Dihedral group of order 6
The smallest non-abelian group has 6 elements. It is a dihedral group with notation D3 (or D6, both are used) and the symmetric group of degree 3, with notation S3.
This page illustrates many group concepts using this group as example.
Contents |
Symmetry groups
In 2D the group D3 is the symmetry group of an equilateral triangle. In contrast with the case of a square or other polygon, all permutations of the vertices can be achieved by rotation and flipping over (or reflecting).
In 3D there are two different symmetry groups which are algebraically the group D3:
- one with a 3-fold rotation axis and a perpendicular 2-fold rotation axis (hence three of these): D3
- one with a 3-fold rotation axis in a plane of reflection (and hence also in two other planes of reflection): C3v
Permutations of a set of three objects
Consider three colored blocks (red, green, and blue), initially placed in the order RGB. Let a be the action "swap the first block and the second block", and let b be the action "swap the second block and the third block".
In multiplicative form, we traditionally write xy for the combined action "first do y, then do x"; so that ab is the action RGB → RBG → BRG, i.e., "take the last block and move it to the front". If we write e for "leave the blocks as they are" (the identity action), then we can write the six permutations of the set of three blocks as the following actions:
- e : RGB → RGB or ()
- a : RGB → GRB or (RG)
- b : RGB → RBG or (GB)
- ab : RGB → BRG or (RBG)
- ba : RGB → GBR or (RGB)
- aba : RGB → BGR or (RB)
Note that the action aa has the effect RGB → GRB → RGB, leaving the blocks as they were; so we can write aa = e. Similarly,
- bb = e,
- (aba)(aba) = e, and
- (ab)(ba) = (ba)(ab) = e;
so each of the above actions has an inverse.
By inspection, we can also determine associativity and closure; note for example that
- (ab)a = a(ba) = aba, and
- (ba)b = b(ab) = aba.
The group is non-abelian since, for example, ab ≠ ba. Since it is built up from the basic actions a and b, we say that the set {a,b} generates it.
The group has presentation
-
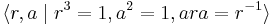 , also written
, also written 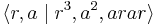
- or
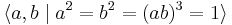 , also written
, also written 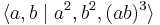
where a and b are swaps and r is a cyclic permutation.
Summary of group operations
With x, y, and z different blocks R, G, and B we have:
- (xyz)(xyz)=(xzy)
- (xyz)(xzy)=()
- (xyz)(xy)=(xz)
- (xy)(xyz)=(yz)
- (xy)(xy)=()
- (xy)(xz)=(xzy)
In the form of a Cayley table:
| * | e | a | b | c | d | f |
|---|---|---|---|---|---|---|
| e | e | a | b | c | d | f |
| a | a | e | d | f | b | c |
| b | b | f | e | d | c | a |
| c | c | d | f | e | a | b |
| d | d | c | a | b | f | e |
| f | f | b | c | a | e | d |
Note that non-equal non-identity elements only commute if they are each other's inverse. Therefore the group is centerless.
Conjugacy classes
We can easily distinguish three kinds of permutations of the three blocks, called conjugacy classes of the group:
- no change (), a group element of order 1
- interchanging two blocks: (RG), (RB), (GB), three group elements of order 2
- a cyclic permutation of all three blocks (RGB), (RBG), two group elements of order 3
For example (RG) and (RB) are both of the form (x y); a permutation of the letters R, G, and B (namely (GB)) changes the notation (RG) into (RB). Therefore, if we apply (GB), then (RB), and then the inverse of (GB), which is also (GB), the resulting permutation is (RG).
Note that conjugate group elements always have the same order, but for groups in general group elements that have the same order need not be conjugate.
Subgroups
From Lagrange's theorem we know that any non-trivial subgroup has order 2 or 3. In fact the two cyclic permutations of all three blocks, with the identity, form a subgroup of order 3, index 2, and the swaps of two blocks, each with the identity, form three subgroups of order 2, index 3.
The first-mentioned is {(),(RGB),(RBG)}, the alternating group A3.
The left cosets and the right cosets of A3 are both that subgroup itself and the three swaps.
The left cosets of {(),(RG)} are:
- that subgroup itself
- {(RB),(RGB)}
- {(GB),(RBG)}
The right cosets of {(RG),()} are:
- that subgroup itself
- {(RBG),(RB)}
- {(RGB),(GB)}
Thus A3 is normal, and the other three non-trivial subgroups are not. The quotient group G / A3 is isomorphic with C2.
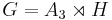 , a semidirect product, where H is a subgroup of two elements: () and one of the three swaps.
, a semidirect product, where H is a subgroup of two elements: () and one of the three swaps.
In terms of permutations the two group elements of G/ A3 are the set of even permutations and the set of odd permutations.
If the original group is that generated by a 120° rotation of a plane about a point, and reflection with respect to a line through that point, then the quotient group has the two elements which can be described as the subsets "just rotate (or do nothing)" and "take a mirror image".
Note that for the symmetry group of a square, an uneven permutation of vertices does not correspond to taking a mirror image, but to operations not allowed for rectangles, i.e. 90° rotation and applying a diagonal axis of reflection.
Semidirect products
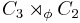 is
is 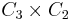 if both φ(0) and φ(1) are the identity. The semidirect product is isomorphic to the dihedral group of order 6 if φ(0) is the identity and φ(1) is the non-trivial automorphism of C3, which inverses the elements.
if both φ(0) and φ(1) are the identity. The semidirect product is isomorphic to the dihedral group of order 6 if φ(0) is the identity and φ(1) is the non-trivial automorphism of C3, which inverses the elements.
Thus we get:
- (n1, 0) * (n2, h2) = (n1 + n2, h2)
- (n1, 1) * (n2, h2) = (n1 - n2, 1 + h2)
for all n1, n2 in C3 and h2 in C2.
In a Cayley table:
00 10 20 01 11 21 00 00 10 20 01 11 21 10 10 20 00 11 21 01 20 20 00 10 21 01 11 01 01 21 11 00 20 10 11 11 01 21 10 00 20 21 21 11 01 20 10 00
Note that for the second digit we essentially have a 2x2 table, with 3x3 equal values for each of these 4 cells. For the first digit the left half of the table is the same as the right half, but the top half is different from the bottom half.
For the direct product the table is the same except that the first digits of the bottom half of the table are the same as in the top half.
Group action
Consider D3 in the geometrical way, as symmetry group of isometries of the plane, and consider the corresponding group action on a set of 30 evenly spaced points on a circle, numbered 0 to 29, with 0 at one of the reflexion axes.
This section illustrates group action concepts for this case.
The action of G on X is called
- transitive if for any two x, y in X there exists an g in G such that g·x = y; - this is not the case
- faithful (or effective) if for any two different g, h in G there exists an x in X such that g·x ≠ h·x; - this is the case, because, except for the identity, symmetry groups do not contain elements that "do nothing"
- free if for any two different g, h in G and all x in X we have g·x ≠ h·x; - this is not the case because there are reflections
Orbits and stabilizers
The orbit of a point x in X is the set of elements of X to which x can be moved by the elements of G. The orbit of x is denoted by Gx:
The orbits are {0,10,20}, {1,9,11,19,21,29}, {2,8,12,18,22,28}, {3,7,13,17,23,27}, {4,6,14,16,24,26}, and {5,15,25}. The points within an orbit are "equivalent". If a symmetry group applies for a pattern, then within each orbit the color is the same.
The set of all orbits of X under the action of G is written as X / G.
If Y is a subset of X, we write GY for the set { g · y : y 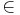 Y and g
Y and g 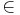 G }. We call the subset Y invariant under G if GY = Y (which is equivalent to GY ⊆ Y). In that case, G also operates on Y. The subset Y is called fixed under G if g · y = y for all g in G and all y in Y. The union of e.g. two orbits is invariant under G, but not fixed.
G }. We call the subset Y invariant under G if GY = Y (which is equivalent to GY ⊆ Y). In that case, G also operates on Y. The subset Y is called fixed under G if g · y = y for all g in G and all y in Y. The union of e.g. two orbits is invariant under G, but not fixed.
For every x in X, we define the stabilizer subgroup of x (also called the isotropy group or little group) as the set of all elements in G that fix x:
If x is a reflection point (0, 5, 10, 15, 20, or 25), its stabilizer is the group of order two containing the identity and the reflection in x. In other cases the stabilizer is the trivial group.
For a fixed x in X, consider the map from G to X given by g |-> g · x. The image of this map is the orbit of x and the coimage is the set of all left cosets of Gx. The standard quotient theorem of set theory then gives a natural bijection between G/Gx and Gx. Specifically, the bijection is given by hGx |-> h · x. This result is known as the orbit-stabilizer theorem. In the two cases of a small orbit, the stabilizer is non-trivial.
If two elements x and y belong to the same orbit, then their stabilizer subgroups, Gx and Gy, are isomorphic. More precisely: if y = g · x, then Gy = gGx g−1. In the example this applies e.g. for 5 and 25, both reflection points. Reflection about 25 corresponds to a rotation of -20, reflection about 3, and rotation of 20.
A result closely related to the orbit-stabilizer theorem is Burnside's lemma:
where Xg is the set of points fixed by g. I.e., the number of orbits is equal to the average number of points fixed per group element.
For the identity all 30 points are fixed, for the two rotations none, and for the three reflections two each: {0,15}, {5,20}, and {10, 25}. Thus the average is six, the number of orbits.