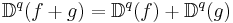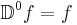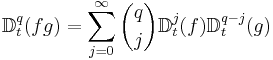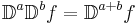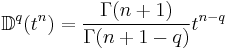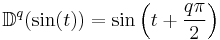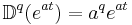Differintegral
In fractional calculus, an area of applied mathematics, the differintegral is a combined differentiation/integration operator. Applied to a function ƒ, the q-differintegral of f, here denoted by
is the fractional derivative (if q>0) or fractional integral (if q<0). If q=0, then the q-th differintegral of a function is the function itself. In the context of fractional integration and differentiation, there are several legitimate definitions of the differintegral.
Contents |
Standard definitions
The three most common forms are:
- This is the simplest and easiest to use, and consequently it is the most often used. It is a generalization of the Cauchy formula for repeated integration to arbitrary order.
- The Grunwald-Letnikov differintegral is a direct generalization of the definition of a derivative. It is more difficult to use than the Riemann-Liouville differintegral, but can sometimes be used to solve problems that the Riemann-Liouville cannot.
- This is formally similar to the Riemann-Liouville differintegral, but applies to periodic functions, with integral zero over a period.
Definitions via transforms
Recall the continuous Fourier transform, here denoted 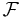 :
:
Using the continuous Fourier transform, in Fourier space, differentiation transforms into a multiplication:
So,
which generalizes to
Under the Laplace transform, here denoted by 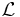 , differentiation transforms into a multiplication
, differentiation transforms into a multiplication
Generalizing to arbitrary order and solving for Dqf(t), one obtains
Basic formal properties
Linearity rules
Zero rule
Product rule
In general, composition (or semigroup) rule
is not satisfied. See Property 2.4 (page 75) in the book A.A. Kilbas, H.M. Srivastava, J.J. Trujillo, Theory and Applications of Fractional Differential Equations. (Elsevier, 2006).
Some basic formulae
See also
References
- "An Introduction to the Fractional Calculus and Fractional Differential Equations", by Kenneth S. Miller, Bertram Ross (Editor), John Wiley & Sons; 1 edition (May 19, 1993). ISBN 0-471-58884-9.
- "The Fractional Calculus; Theory and Applications of Differentiation and Integration to Arbitrary Order (Mathematics in Science and Engineering, V)", by Keith B. Oldham, Jerome Spanier, Academic Press; (November 1974). ISBN 0-12-525550-0.
- "Fractional Differential Equations. An Introduction to Fractional Derivatives, Fractional Differential Equations, Some Methods of Their Solution and Some of Their Applications", (Mathematics in Science and Engineering, vol. 198), by Igor Podlubny, Academic Press (October 1998). ISBN 0-12-558840-2.
- "Fractals and Fractional Calculus in Continuum Mechanics", by A. Carpinteri (Editor), F. Mainardi (Editor), Springer-Verlag Telos; (January 1998). ISBN 3-211-82913-X.
- "Physics of Fractal Operators", by Bruce J. West, Mauro Bologna, Paolo Grigolini, Springer Verlag; (January 14, 2003). ISBN 0-387-95554-2
- Operator of fractional derivative in the complex plane, by Petr Zavada, Commun.Math.Phys.192, pp. 261-285,1998. doi:10.1007/s002200050299 (available online or as the arXiv preprint)
- Relativistic wave equations with fractional derivatives and pseudodifferential operators, by Petr Zavada, Journal of Applied Mathematics, vol. 2, no. 4, pp. 163-197, 2002. doi:10.1155/S1110757X02110102 (available online or as the arXiv preprint)
External links
- MathWorld - Fractional calculus
- MathWorld - Fractional derivative
- Specialized journal: Fractional Calculus and Applied Analysis
- Specialized journal: Fractional Dynamic Systems (FDS)
- Specialized journal: Communications in Fractional Calculus (ISSN 2218-3892)
- http://www.nasatech.com/Briefs/Oct02/LEW17139.html
- http://unr.edu/homepage/mcubed/FRG.html
- Igor Podlubny's collection of related books, articles, links, software, etc.
- Podlubny, I., Geometric and physical interpretation of fractional integration and fractional differentiation. Fractional Calculus and Applied Analysis, vol. 5, no. 4, 2002, 367–386. (available as original article, or preprint at Arxiv.org)
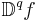
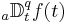
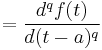
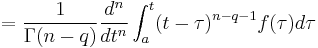
![=\lim_{N \to \infty}\left[\frac{t-a}{N}\right]^{-q}\sum_{j=0}^{N-1}(-1)^j{q \choose j}f\left(t-j\left[\frac{t-a}{N}\right]\right)](/2012-wikipedia_en_all_nopic_01_2012/I/3cbc9b2dc7c169605bf1c21736f296bc.png)
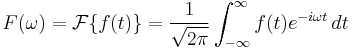
![\mathcal{F}\left[\frac{df(t)}{dt}\right] = i \omega \mathcal{F}[f(t)]](/2012-wikipedia_en_all_nopic_01_2012/I/fbd542ad2102f1bc8bda75f20d4ad1f1.png)
![\frac{d^nf(t)}{dt^n} = \mathcal{F}^{-1}\left\{(i \omega)^n\mathcal{F}[f(t)]\right\}](/2012-wikipedia_en_all_nopic_01_2012/I/2121401ae364c8fa22efb0cc13e4d343.png)
![\mathbb{D}^qf(t)=\mathcal{F}^{-1}\left\{(i \omega)^q\mathcal{F}[f(t)]\right\}.](/2012-wikipedia_en_all_nopic_01_2012/I/ab15d011865194401ccd467e24a24d18.png)
![\mathcal{L}\left[\frac{df(t)}{dt}\right] = s\mathcal{L}[f(t)].](/2012-wikipedia_en_all_nopic_01_2012/I/37b251ddd1c65b06c4d6f16e90f7897f.png)
![\mathbb{D}^qf(t)=\mathcal{L}^{-1}\left\{s^{q}\mathcal{L}[f(t)]\right\}.](/2012-wikipedia_en_all_nopic_01_2012/I/c08bbf4d4ab30c2e45435727a586992c.png)