Differential game
In game theory, differential games are a group of problems related to the modeling and analysis of conflict in the context of a dynamical system. The problem usually consists of two actors, a pursuer and an evader, with conflicting goals. The dynamics of the pursuer and the evader are modeled by systems of differential equations.
Differential games are related closely with optimal control problems. In an optimal control problem there is single control 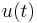 and a single criterion to be optimized; differential game theory generalizes this to two controls
and a single criterion to be optimized; differential game theory generalizes this to two controls 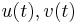 and two criteria, one for each player. Each player attempts to control the state of the system so as to achieve his goal; the system responds to the inputs of both players.
and two criteria, one for each player. Each player attempts to control the state of the system so as to achieve his goal; the system responds to the inputs of both players.
The first to study differential games was Rufus Isaacs (1951, published 1965)[1] and one of the first games analyzed was the 'homicidal chauffeur game'.
Differential games have been applied to economics. Recent developments include adding stochasticity to differential games and the derivation of the stochastic feedback Nash equilibrium (SFNE). A recent example is the stochastic differential game of capitalism by Leong and Huang (2010)[2].
Applications
For a survey of pursuit-evasion differential games see Pachter.[3]
Notes
- ^ Rufus Isaacs, Differential Games, Dover, 1999. ISBN 0486406822 Google Books
- ^ Leong, C.K. and W. Huang, “A Stochastic Differential Game of Capitalism”, Journal of Mathematical Economics, 46(4), 2010, pp. 552-561
- ^ Meir Pachter: Simple-motion pursuit-evasion differential games, 2002