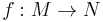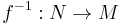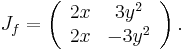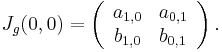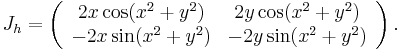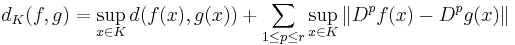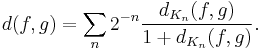Diffeomorphism

In mathematics, a diffeomorphism is an isomorphism in the category of smooth manifolds. It is an invertible function that maps one differentiable manifold to another, such that both the function and its inverse are smooth.

1 Definition
2 Diffeomorphisms of subsets of manifolds
3 Local description
4 Examples
5 Diffeomorphism group
6 Homeomorphism and diffeomorphism
7 See also
8 Notes
9 References

Definition

Given two manifolds M and N, a bijective map $f$ from M to N is called a diffeomorphism if both

$f:M\to N$

and its inverse

$f^{-1}:N\to M$

are differentiable (if these functions are r times continuously differentiable, f is called a 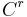$C^r$ -diffeomorphism).

Two manifolds M and N are diffeomorphic (symbol usually being 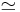$\simeq$ ) if there is a smooth bijective map $f$ from M to N with a smooth inverse. They are 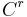$C^r$ diffeomorphic if there is an r times continuously differentiable bijective map between them whose inverse is also r times continuously differentiable.

Diffeomorphisms of subsets of manifolds

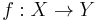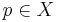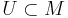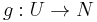Given a subset X of a manifold M and a subset Y of a manifold N, a function $f�: X \to Y$ is said to be smooth if for all $p \in X$ there is a neighborhood $U \subset M$ of $p$ and a smooth function $g�: U \to N$ such that the restrictions agree 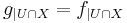$g_{|U \cap X} = f_{|U \cap X}$ (note that g is an extension of f). We say that $f$ is a diffeomorphism if it is bijective, smooth, and if its inverse is smooth.

Local description

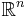Model example: if $U$ and $V$ are two connected open subsets of $\mathbb{R}^n$ such that $V$ is simply connected, a differentiable map $f$ from $U$ to $V$ is a diffeomorphism if it is proper and if

the differential 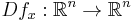$Df_x�: \mathbb{R}^n \to \mathbb{R}^n$ is bijective at each point $x\in U$ .

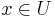Remarks

It is essential for U to be simply connected for the function to be globally invertible (under the sole condition that its derivative is a bijective map at each point).
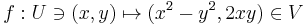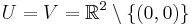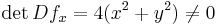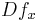- For example, consider the map $f:U\ni(x,y)\mapsto(x^2-y^2,2xy)\in V$ (which is the "realification" of the complex square function) where $U=V=\mathbb{R}^2\setminus\{(0,0)\}$ . Then the map $f$ is surjective and its satisfies $\det Df_x=4(x^2%2By^2)\neq0$ (thus $Df_x$ is bijective at each point) yet $f$ is not invertible, because it fails to be injective, e.g., 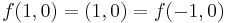$f(1,0)=(1,0)=f(-1,0)$ .
Since the differential at a point (for a differentiable function) 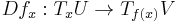$Df_x�: T_xU \to T_{f(x)}V$ is a linear map it has a well defined inverse if, and only if, 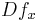$Df_x$ is a bijection. The matrix representation of 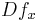$Df_x$ is the 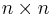$n \times n$ matrix of first order partial derivatives whose entry in the i-th row and j-th colomn is 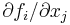$\partial f_i / \partial x_j$ . We often use this so-called Jacobian matrix for explicit computations.
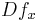Diffeomorphisms are necessarily between manifolds of the same dimension. Imagine that f were going from dimension $n$ to dimension $k$ . If n < k then $Df_x$ could never be surjective, and if n > k then 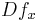$Df_x$ could never be injective. So in both cases 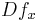$Df_x$ fails to be a bijection.
If 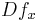$Df_x$ is a bijection at x then we say that f is a local diffeomorphism (since by continuity 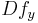$Df_y$ will also be bijective for all y sufficiently close to x). If 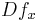$Df_x$ is a bijection for all x then we say that f is a (global) diffeomorphism.
Given a smooth map from dimension n to dimension k, if Df (resp. 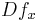$Df_x$ ) is surjective then we say that f is a submersion (resp. local submersion), and if Df (resp. 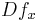$Df_x$ ) is injective we say that f is an immersion (resp. local immersion).
A differentiable bijection is not necessarily a diffeomorphism, e.g. 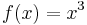$f(x)=x^3$ is not a diffeomorphism from $\mathbb{R}$ to itself because its derivative vanishes at 0 (and hence its inverse is not differentiable at 0). This is an example of a homeomorphism that is not a diffeomorphism.
f being a diffeomorphism is a stronger condition than f being a homeomorphism (when f is a map between differentiable manifolds). For a diffeomorphism we need f and its inverse to be differentiable. For a homeomorphism we only require that f and its inverse be continuous. Thus every diffeomorphism is a homeomorphism, but the converse is false: not every homeomorphism is a diffeomorphism.

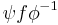Now, $f$ from M to N is called a diffeomorphism if in coordinates charts it satisfies the definition above. More precisely, pick any cover of M by compatible coordinate charts, and do the same for N. Let $\phi$ and $\psi$ be charts on M and N respectively, with $U$ being the image of $\phi$ and $V$ the image of $\psi$ . Then the conditions says that the map $\psi f \phi^{-1}$ from $U$ to $V$ is a diffeomorphism as in the definition above (whenever it makes sense). One has to check that for every couple of charts $\phi$ , $\psi$ of two given atlases, but once checked, it will be true for any other compatible chart. Again we see that dimensions have to agree.

Examples

Since any manifold can be locally parametrised, we can consider some explicit maps from two-space into two-space.

Let 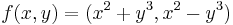$f(x,y) = (x^2 %2B y^3, x^2 - y^3)$ . We can calculate the Jacobian matrix:

$J_f = \left( \begin{array}{cc} 2x & 3y^2 \\ 2x & -3y^2 \end{array} \right) .$

The Jacobian matrix has zero determinant if, and only if. 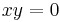$xy = 0$ . We see that f is a diffeomorphism away from the x-axis and the y-axis.

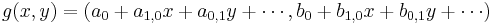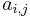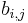Let $g(x,y) = (a_0 %2B a_{1,0}x %2B a_{0,1}y %2B \cdots, b_0 %2B b_{1,0}x %2B b_{0,1}y %2B \cdots)$ where the $a_{i,j}$ and $b_{i,j}$ are arbitrary real numbers, and the omitted terms are of degree at least two in x and y. We can calculate the Jacobian matrix at 0:

$J_g(0,0) = \left( \begin{array}{cc} a_{1,0} & a_{0,1} \\ b_{1,0} & b_{0,1} \end{array}\right).$

We see that g is a local diffeomorphism at 0 if, and only if, 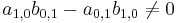$a_{1,0}b_{0,1} - a_{0,1}b_{1,0} \neq 0$ , i.e. the linear terms in the components of g are linearly independent as polynomials.

Now let 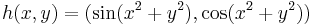$h(x,y) = (\sin(x^2 %2B y^2), \cos(x^2 %2B y^2))$ . We can calculate the Jacobian matrix:

$J_h = \left( \begin{array}{cc} 2x\cos(x^2 %2B y^2) & 2y\cos(x^2 %2B y^2) \\ -2x\sin(x^2%2By^2) & -2y\sin(x^2 %2B y^2) \end{array} \right) .$

The Jacobian matrix has zero determinant everywhere! In fact we see that the image of h is the unit circle.

Diffeomorphism group

Let M be a differentiable manifold that is second-countable and Hausdorff. The diffeomorphism group of M is the group of all C^r diffeomorphisms of M to itself, and is denoted by Diff^r(M) or Diff(M) when r is understood. This is a 'large' group, in the sense that it is not locally compact (provided M is not zero-dimensional).

Topology

The diffeomorphism group has two natural topologies, called the weak and strong topology (Hirsch 1997). When the manifold is compact, these two topologies agree. The weak topology is always metrizable. When the manifold is not compact, the strong topology captures the behavior of functions "at infinity", and is not metrizable. It is, however, still Baire.

Fixing a Riemannian metric on M, the weak topology is the topology induced by the family of metrics

$d_K(f,g) = \sup_{x\in K} d(f(x),g(x)) %2B \sum_{1\le p\le r} \sup_{x\in K}\|D^pf(x) - D^pg(x)\|$

as K varies over compact subsets of M. Indeed, since M is σ-compact, there is a sequence of compact subsets K_n whose union is M. Then, define

$d(f,g) = \sum_n 2^{-n}\frac{d_{K_n}(f,g)}{1%2Bd_{K_n}(f,g)}.$

The diffeomorphism group equipped with its weak topology is locally homeomorphic to the space of C^r vector fields (Leslie 1967). Over a compact subset of M, this follows by fixing a Riemannian metric on M and using the exponential map for that metric. If r is finite and the manifold is compact, the space of vector fields is a Banach space. Moreover, the transition maps from one chart of this atlas to another are smooth, making the diffeomorphism group into a Banach manifold. If r = ∞ or if the manifold is σ-compact, the space of vector fields is a Fréchet space. Moreover, the transition maps are smooth, making the diffeomorphism group into a Fréchet manifold.

Examples

When M = G is a Lie group, there is a natural inclusion of G in its own diffeomorphism group via left-translation. Let Diff(G) denote the diffeomorphism group of G, then there is a splitting Diff(G) ≃ G × Diff(G,e) where Diff(G,e) is the subgroup of Diff(G) that fixes the identity element of the group.

The diffeomorphism group of Euclidean space Rⁿ consists of two components, consisting of the orientation preserving and orientation reversing diffeomorphisms. In fact, the general linear group is a deformation retract of subgroup Diff(Rⁿ,0) of diffeomorphisms fixing the origin under the map ƒ(x) ↦ ƒ(tx)/t, t ∈ (0,1]. Hence, in particular, the general linear group is also a deformation retract of the full diffeomorphism group as well.

For a finite set of points, the diffeomorphism group is simply the symmetric group. Similarly, if M is any manifold there is a group extension 0 → Diff₀(M) → Diff(M) → Σ(π₀M). Here Diff₀(M)is the subgroup of 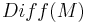$Diff(M)$ that preserves all the components of M, and Σ(π₀M) is the permutation group of the set π₀M (the components of M). Moreover, the image of the map Diff(M) → Σ(π₀M) is the bijections of π₀M that preserve diffeomorphism classes.

Transitivity

For a connected manifold M the diffeomorphism group acts transitively on M. More generally, the diffeomorphism group acts transitively on the configuration space C_kM. If the dimension of M is at least two the diffeomorphism group acts transitively on the configuration space F_kM: the action on M is multiply transitive (Banyaga 1997, p. 29).

Extensions of diffeomorphisms

In 1926, Tibor Radó asked whether the harmonic extension of any homeomorphism (or diffeomorphism) of the unit circle to the unit disc yields a diffeomorphism on the open disc. An elegant proof was provided shortly afterwards by Hellmuth Kneser and a completely different proof was discovered in 1945 by Gustave Choquet, apparently unaware that the theorem was already known.

The (orientation-preserving) diffeomorphism group of the circle is pathwise connected. This can be seen by noting that any such diffeomorphism can be lifted to a diffeomorphism f of the reals satisfying f(x+1) = f(x) +1; this space is convex and hence path connected. A smooth eventually constant path to the identity gives a second more elementary way of extending a diffeomorphism from the circle to the open unit disc (this is a special case of the Alexander trick). Moreover, the diffeomorphism group of the circle has the homotopy-type of the orthogonal group 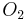$O_2$ .

The corresponding extension problem for diffeomorphisms of higher dimensional spheres Sⁿ⁻¹ was much studied in the 1950s and 1960s, with notable contributions from René Thom, John Milnor and Stephen Smale. An obstruction to such extensions is given by the finite Abelian group Γ_n, the "group of twisted spheres", defined as the quotient of the Abelian component group of the diffeomorphism group by the subgroup of classes extending to diffeomorphisms of the ball Bⁿ.

Connectedness

For manifolds the diffeomorphism group is usually not connected. Its component group is called the mapping class group. In dimension 2, i.e. for surfaces, the mapping class group is a finitely presented group, generated by Dehn twists (Dehn, Lickorish, Hatcher). Max Dehn and Jakob Nielsen showed that it can be identified with the outer automorphism group of the fundamental group of the surface.

William Thurston refined this analysis by classifying elements of the mapping class group into three types: those equivalent to a periodic diffeomorphism; those equivalent to a diffeomorphism leaving a simple closed curve invariant; and those equivalent to pseudo-Anosov diffeomorphisms. In the case of the torus S¹ x S¹ = R²/Z², the mapping class group is just the modular group SL(2,Z) and the classification reduces to the classical one in terms of elliptic, parabolic and hyperbolic matrices. Thurston accomplished his classification by observing that the mapping class group acted naturally on a compactification of Teichmüller space; since this enlarged space was homeomorphic to a closed ball, the Brouwer fixed-point theorem became applicable.

If M is an oriented smooth closed manifold, it was conjectured by Smale that the identity component of the group of orientation-preserving diffeomorphisms is simple. This had first been proved for a product of circles by Michel Herman; it was proved in full generality by Thurston.

Homotopy types

The diffeomorphism group of 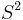$S^2$ has the homotopy-type of the subgroup 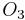$O_3$ . This was proven by Steve Smale.^[1]

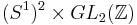The diffeomorphism group of the torus has the homotopy-type of its linear automorphisms: $(S^1)^2 \times GL_2(\mathbb Z)$ .

The diffeomorphism groups of orientable surfaces of genus 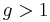$g > 1$ have the homotopy-type of their mapping class groups—i.e.: the components are contractible.

The homotopy-type of the diffeomorphism groups of 3-manifolds are fairly well-understood via the work of Ivanov, Hatcher, Gabai and Rubinstein although there are a few outstanding open cases, primarily 3-manifolds with finite fundamental groups.

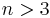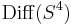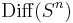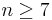The homotopy-type of diffeomorphism groups of n-manifolds for $n>3$ are poorly undersood. For example, it is an open problem whether or not $\mathrm{Diff}(S^4)$ has more than two components. But via the work of Milnor, Kahn and Antonelli it's known that $\mathrm{Diff}(S^n)$ does not have the homotopy-type of a finite CW-complex provided $n \geq 7$ .

Homeomorphism and diffeomorphism

It is easy to find a homeomorphism that is not a diffeomorphism, but it is more difficult to find a pair of homeomorphic manifolds that are not diffeomorphic. In dimensions 1, 2, 3, any pair of homeomorphic smooth manifolds are diffeomorphic. In dimension 4 or greater, examples of homeomorphic but not diffeomorphic pairs have been found. The first such example was constructed by John Milnor in dimension 7. He constructed a smooth 7-dimensional manifold (called now Milnor's sphere) that is homeomorphic to the standard 7-sphere but not diffeomorphic to it. There are in fact 28 oriented diffeomorphism classes of manifolds homeomorphic to the 7-sphere (each of them is a total space of the fiber bundle over the 4-sphere with the 3-sphere as the fiber).

Much more extreme phenomena occur for 4-manifolds: in the early 1980s, a combination of results due to Simon Donaldson and Michael Freedman led to the discovery of exotic R4s: there are uncountably many pairwise non-diffeomorphic open subsets of 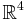$\mathbb{R}^4$ each of which is homeomorphic to 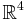$\mathbb{R}^4$ , and also there are uncountably many pairwise non-diffeomorphic differentiable manifolds homeomorphic to 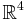$\mathbb{R}^4$ that do not embed smoothly in $\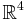mathbb{R}^4$ .

Notes

^ Smale, Diffeomorphisms of the 2-sphere, Proc. Amer. Math. Soc. 10 (1959) 621–626.

References

Chaudhuri, Shyamoli, Hakuru Kawai and S.-H Henry Tye. "Path-integral formulation of closed strings," Phys. Rev. D, 36: 1148, 1987.

Banyaga, Augustin (1997), The structure of classical diffeomorphism groups, Mathematics and its Applications, 400, Kluwer Academic, ISBN 0-7923-4475-8

Duren, Peter L. (2004), Harmonic Mappings in the Plane, Cambridge Mathematical Tracts, 156, Cambridge University Press, ISBN 0521641217

Hirsch, Morris (1997), Differential Topology, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90148-0

Kriegl, Andreas; Michor, Peter (1997), The convenient setting of global analysis, Mathematical Surveys and Monographs, 53, American Mathematical Society, ISBN 0-8218-0780-3

Leslie, J. A. (1967), "On a differential structure for the group of diffeomorphisms", Topology. an International Journal of Mathematics 6 (2): 263–271, doi:10.1016/0040-9383(67)90038-9, ISSN 0040-9383, MR 0210147

Milnor, John W. (2007), Collected Works Vol. III, Differential Topology, American Mathematical Society, ISBN 0821842307

Omori, Hideki (1997), Infinite-dimensional Lie groups, Translations of Mathematical Monographs, 158, American Mathematical Society, ISBN 0-8218-4575-6

Kneser, Hellmuth (1926), "Lösung der Aufgabe 41." (in German), Jahresbericht der Deutschen Mathematiker-Vereinigung 35 (2): 123f.

Diffeomorphism

Contents

Definition

Diffeomorphisms of subsets of manifolds

Local description

Examples

Diffeomorphism group

Topology

Examples

Transitivity

Extensions of diffeomorphisms

Connectedness

Homotopy types

Homeomorphism and diffeomorphism

See also

Notes

References