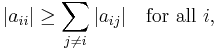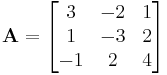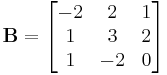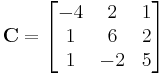Diagonally dominant matrix
In mathematics, a matrix is said to be diagonally dominant if for every row of the matrix, the magnitude of the diagonal entry in a row is larger than or equal to the sum of the magnitudes of all the other (non-diagonal) entries in that row. More precisely, the matrix A is diagonally dominant if
where aij denotes the entry in the ith row and jth column.
Note that this definition uses a weak inequality, and is therefore sometimes called weak diagonal dominance. If a strict inequality (>) is used, this is called strict diagonal dominance. The unqualified term diagonal dominance can mean both strict and weak diagonal dominance, depending on the context.[1]
Contents |
Variations
The definition in the first paragraph sums entries across rows. It is therefore sometimes called row diagonal dominance. If one changes the definition to sum down columns, this is called column diagonal dominance.
If an irreducible matrix is weakly diagonally dominant, but in at least one row (or column) is strictly diagonally dominant, then the matrix is irreducibly diagonally dominant.
Examples
The matrix
gives
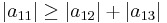 since
since 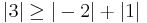
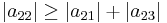 since
since 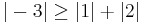
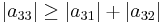 since
since 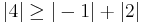 .
.
Because the magnitude of each diagonal element is greater than or equal to the sum of the magnitude of other elements in the row, A is diagonally dominant.
The matrix
But here,
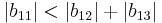 since
since 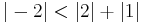
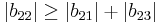 since
since 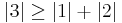
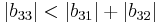 since
since 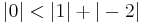 .
.
Because 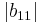 and
and 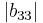 are less than the sum of the magnitude of other elements in their respective row, B is not diagonally dominant.
are less than the sum of the magnitude of other elements in their respective row, B is not diagonally dominant.
The matrix
gives
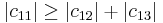 since
since 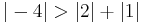
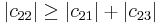 since
since 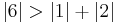
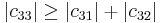 since
since 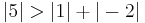 .
.
Because the magnitude of each diagonal element is greater than the sum of the magnitude of the other elements in the row, C is strictly diagonally dominant.
Applications and properties
By the Gershgorin circle theorem, a strictly (or irreducibly) diagonally dominant matrix is non-singular. This result is known as the Levy–Desplanques theorem.[2]
A Hermitian diagonally dominant matrix with real non-negative diagonal entries is positive semi-definite. If the symmetry requirement is eliminated, such a matrix is not necessarily positive semi-definite; however, the real parts of its eigenvalues are non-negative.
No (partial) pivoting is necessary for a strictly column diagonally dominant matrix when performing Gaussian elimination (LU factorization).
The Jacobi and Gauss–Seidel methods for solving a linear system converge if the matrix is strictly (or irreducibly) diagonally dominant. In October 2010, researchers at Carnegie Mellon University announced that they have discovered a new algorithm for solving symmetric diagonally dominant linear systems.[3]
Many matrices that arise in finite element methods are diagonally dominant.
A slight variation on the idea of diagonal dominance is used to prove that the pairing on diagrams without loops in the Temperley–Lieb algebra is nondegenerate.[4] For a matrix with polynomial entries, one sensible definition of diagonal dominance is if the highest power of  appearing in each row appears only on the diagonal. (The evaluations of such a matrix at large values of
appearing in each row appears only on the diagonal. (The evaluations of such a matrix at large values of  are diagonally dominant in the above sense.)
are diagonally dominant in the above sense.)
Links
- PlanetMath: Diagonal dominance definition
- PlanetMath: Properties of diagonally dominant matrices
- Mathworld
Notes
- ^ For instance, Horn and Johnson (1985, p. 349) use it to mean weak diagonal dominance.
- ^ Horn and Johnson, Thm 6.1.10. This result has been independently rediscovered dozens of times. A few notable ones are Lévy (1881), Desplanques (1886), Minkowski (1900), Hadamard (1903), Schur, Markov (1908), Rohrbach (1931), Gershgorin (1931), Artin (1932), Ostrowski (1937), and Furtwängler (1936). For a history of this "recurring theorem" see: Taussky, Olga (1949). "A recurring theorem on determinants". American Mathematical Monthly (The American Mathematical Monthly, Vol. 56, No. 10) 56 (10): 672–676. doi:10.2307/2305561. JSTOR 2305561. Another useful history is in: Schneider, Hans (1977). "Olga Taussky-Todd's influence on matrix theory and matrix theorists". Linear and Multilinear Algebra 5 (3): 197–224. doi:10.1080/03081087708817197.
- ^ http://www.pcpro.co.uk/news/362170/algorithm-sees-massive-leap-in-complex-number-crunching
- ^ K.H. Ko and L. Smolinski (1991). "A combinatorial matrix in 3-manifold theory". Pacific. J. Math. 149: 319–336.
References
- Gene H. Golub & Charles F. Van Loan. Matrix Computations, 1996. ISBN 0-8018-5414-8
- Roger A. Horn & Charles R. Johnson. Matrix Analysis, Cambridge University Press, 1985. ISBN 0-521-38632-2 (paperback).
|
||||||||||||||