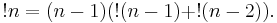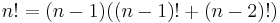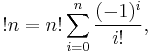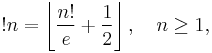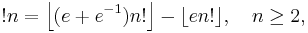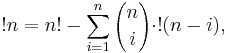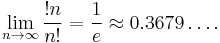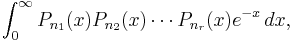Derangement

For the psychological condition, see psychosis.

In combinatorial mathematics, a derangement is a permutation of the elements of a set such that none of the elements appear in their original position.

The numbers of derangements !n for sets of size n are called "de Montmort numbers" or "derangement numbers" (and can be generalized to rencontres numbers); the subfactorial function (not to be confused with the factorial n!) maps n to !n. No standard notation for subfactorials is agreed upon, and n¡ is sometimes used instead of !n.[1]

The problem of counting derangements was first considered by Pierre Raymond de Montmort[2] in 1708; he solved it in 1713, as did Nicholas Bernoulli at about the same time.

Contents

Example

Suppose that a professor has graded 4 tests for 4 students -- student A, student B, student C, and student D. However, the professor mixed up the tests when handing them back, and now none of the students has the correct test. How many ways could the professor have mixed them all up in this way? Out of 24 possible permutations for handing back the tests, there are only 9 derangements:

BADC, BCDA, BDAC,
CADB, CDAB, CDBA,
DABC, DCAB, DCBA.

In every other permutation of this 4-member set, at least one student gets the right test.

Another version of the problem arises when we ask for the number of ways n letters, each addressed to a different person, can be placed in n pre-addressed envelopes so that no letter appears in the correctly addressed envelope.

Counting derangements

Suppose that there are n persons numbered 1, 2, ..., n. Let there be n hats also numbered 1, 2, ..., n. We have to find the number of ways in which no one gets the hat having same number as his/her number. Let us assume that first person takes the hat i. There are n − 1 ways for the first person to choose the number i. Now there are 2 options:

  1. Person i does not take the hat 1. This case is equivalent to solving the problem with n − 1 persons n − 1 hats: each of the remaining n − 1 people has precisely 1 forbidden choice from among the remaining n − 1 hats (i's forbidden choice is hat 1).
  2. Person i takes the hat of 1. Now the problem reduces to n − 2 persons and n − 2 hats.

From this, the following relation is derived:

!n = (n - 1) (!(n-1) %2B�!(n-2)).\,

Notice that this same recurrence formula also works for factorials with different starting values. That is 0! = 1, 1! = 1 and

n! = (n - 1) ((n-1)! %2B (n-2)!)\,

which is helpful in proving the limit relationship with e below.

Also, the following formulas are known:[3]

!n = n! \sum_{i=0}^n \frac{(-1)^i}{i!},
!n = \left\lfloor\frac{n!}{e}%2B\frac{1}{2}\right\rfloor , \quad n\geq 1,
!n = \left\lfloor(e%2Be^{-1})n!\right\rfloor-\lfloor en!\rfloor , \quad n\geq 2,
!n = n! - \sum_{i=1}^n {n \choose i} \cdot�!(n-i),

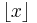where \left\lfloor x \right\rfloor is the floor function. Starting with n = 0, the numbers of derangements of n are:

1, 0, 1, 2, 9, 44, 265, 1854, 14833, 133496, 1334961, 14684570, 176214841, 2290792932, ... (sequence A000166 in OEIS).

These numbers are also called subfactorial or rencontres numbers.

Perhaps a more well-known method of counting derangements uses the inclusion-exclusion principle.

Limit as n approaches ∞

Using this recurrence, it can be shown that, in the limit,

\lim_{n\to\infty} {!n \over n!} = {1 \over e} \approx 0.3679\dots.

This is the limit of the probability pn = dn/n! that a randomly selected permutation is a derangement. The probability approaches this limit quite quickly.

More information about this calculation and the above limit may be found on the page on the statistics of random permutations.

Generalizations

The problème des rencontres asks how many permutations of a size-n set have exactly k fixed points.

Derangements are an example of the wider field of constrained permutations. For example, the ménage problem asks if n married couples are seated boy-girl-boy-girl-... around a circular table, how many ways can they be seated so that no man is seated next to his wife?

More formally, given sets A and S, and some sets U and V of surjections A → S, we often wish to know the number of pairs of functions (f, g) such that f is in U and g is in V, and for all a in A, f(a) ≠ g(a); in other words, where for each f and g, there exists a derangement φ of S such that f(a) = φ(g(a)).

Another generalization is the following problem:

How many anagrams with no fixed letters of a given word are there?

For instance, for a word made of only two different letters, say n letters A and m letters B, the answer is, of course, 1 or 0 according whether n = m or not, for the only way to form an anagram without fixed letters is to exchange all the A with B, which is possible if and only if n = m. In the general case, for a word with n1 letters X1, n2 letters X2, ..., nr letters Xr it turns out (after a proper use of the inclusion-exclusion formula) that the answer has the form:

\int_0^\infty P_{n_1} (x) P_{n_2}(x)\cdots P_{n_r}(x) e^{-x}\, dx,

for a certain sequence of polynomials Pn, where Pn has degree n. But the above answer for the case r = 2 gives an orthogonality relation, whence the Pn's are the Laguerre polynomials (up to a sign that is easily decided).[4]

References

  1. ^ Ronald L. Graham, Donald E. Knuth, Oren Patashnik, Concrete Mathematics (1994), Addison-Wesley, Reading MA. ISBN 0201558025
  2. ^ de Montmort, P. R. (1708). Essay d'analyse sur les jeux de hazard. Paris: Jacque Quillau. Seconde Edition, Revue & augmentée de plusieurs Lettres. Paris: Jacque Quillau. 1713.
  3. ^ Hassani, M. "Derangements and Applications." J. Integer Seq. 6, No. 03.1.2, 1–8, 2003
  4. ^ Even, S.; J. Gillis (1976). "Derangements and Laguerre polynomials". Mathematical Proceedings of the Cambridge Philosophical Society 79 (01): 135-143. doi:10.1017/S0305004100052154. http://journals.cambridge.org/action/displayAbstract?fromPage=online&aid=2128316. Retrieved 27 December 2011. 

External links