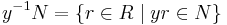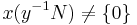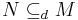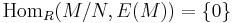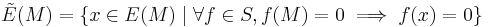Dense submodule
In abstract algebra, specifically in module theory, a dense submodule of a module is a refinement of the notion of an essential submodule. If N is a dense submodule of M, it may also be said it may alternatively be said that "N ⊆ M is a rational extension". Dense submodules are connected with rings of quotients in noncommutative ring theory. Most of the results appearing here were first established in (Johnson 1951), (Utumi 1956) and (Findlay & Lambek 1958).
It should be noticed that this terminology is different from the notion of a dense subset in general topology. No topology is needed to define a dense submodule, and a dense submodule may or may not be topologically dense in a module with topology.
Contents |
Definition
This article modifies exposition appearing in (Storrer 1972) and (Lam 1999, p. 272). Let R be a ring, and M be a right R module with submodule N. For an element y of M, define
Note that the expression y−1 is only formal and that y is not necessarily invertible, but it helps to suggest that y⋅(y−1N) ⊆ N. The set y −1N is always a right ideal of R.
A submodule N of M is said to be a dense submodule if for all x and y in M with x ≠ 0, there exists an r in R such that xr ≠ {0} and yr is in N. In other words, using the introduced notation, the set
In this case, the relationship is denoted by
Another equivalent definition is homological in nature: N is dense in M if and only if
where E(M) is the injective hull of M.
Properties
- It can be shown that N is an essential submodule of M if and only if for all y ≠ 0 in M, the set y⋅(y −1N) ≠ {0}. Clearly then, every dense submodule is an essential submodule.
- If M is a nonsingular module, then N is dense in M if and only if it is essential in M.
- A ring is a right nonsingular ring if and only if its essential right ideals are all dense right ideals.
- If N and N' are dense submodules of M, then so is N ∩ N' .
- If N is dense and N ⊆ K ⊆ M, then K is also dense.
- If B is a dense right ideal in R, then so is y−1B for any y in R.
Examples
- If x is a non-zerodivisor in the center of R, then xR is a dense right ideal of R.
- If I is a two-sided ideal of R, I is dense as a right ideal if and only if the left annihilator of I is zero, that is,
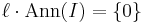 . In particular in commutative rings, the dense ideals are precisely the ideals which are faithful modules.
. In particular in commutative rings, the dense ideals are precisely the ideals which are faithful modules.
Applications
Rational hull of a module
Every right R module M has a maximal essential extension E(M) which is its injective hull. The analogous construction using a maximal dense extension results in the rational hull Ẽ(M) which is a submodule of E(M). When a module has no proper rational extension, so that Ẽ(M) = M, the module is said to be rationally complete. If R is right nonsingular, then of course Ẽ(M) = E(M).
The rational hull is readily identified within the injective hull. Let S=EndR(E(M)) be the endomorphism ring of the injective hull. Then an element x of the injective hull is in the rational hull if and only if x is sent to zero by all maps in S which are zero on M. In symbols,
In general, there may be maps in S which are zero on M and yet are nonzero for some x not in M, and such an x would not be in the rational hull.
Maximal right ring of quotients
The maximal right ring of quotients can be described in two ways in connection with dense right ideals of R.
- In one method, Ẽ(R) is shown to be module isomorphic to a certain endomorphism ring, and the ring structure is taken across this isomorphism to imbue Ẽ(R) with a ring structure, that of the maximal right ring of quotients. (Lam 1999, p. 366)
- In a second method, the maximal right ring of quotients is identified with a set of equivalence classes of homomorphisms from dense right ideals of R into R. The equivalence relation says that two functions are equivalent if they agree on a dense right ideal of R. (Lam 1999, p. 370)
References
- Findlay, G. D.; Lambek, J. (1958), "A generalized ring of quotients. I, II", Canad. Math. Bull. 1: 77–85, 155–167, ISSN 0008-439, MR(20 #888) 0094370 (20 #888)
- Johnson, R. E. (1951), "The extended centralizer of a ring over a module", Proc. Amer. Math. Soc. 2: 891–895, ISSN 0002-9939, MR(13,618c) 0045695 (13,618c)
- Lam, Tsit-Yuen (1999), Lectures on modules and rings, Graduate Texts in Mathematics No. 189, Berlin, New York: Springer-Verlag, ISBN 978-0-387-98428-5, MR1653294
- Storrer, Hans H. (1972), "On Goldman's primary decomposition", Lecutres on rings and modules (Tulane Univ. Ring and Operator Theory) (Berlin: Springer) I: 617–661. Lecture Notes in Math., Vol. 246, MR(50 #13164) 0360717 (50 #13164)
- Utumi, Yuzo (1956), "On quotient rings", Osaka Math. J. 8: 1–18, MR(18,7c) 0078966 (18,7c)