Dehn surgery
In topology, a branch of mathematics, a Dehn surgery, named after Max Dehn, is a specific construction used to modify 3-manifolds. The process takes as input a 3-manifold together with a link. Dehn surgery can be thought of as a two stage process: drilling and Dehn filling.
Contents |
Definitions
- Given a 3-manifold
 and a link
and a link 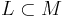 ,
,  drilled along
drilled along  is obtained by removing an open tubular neighborhood of
is obtained by removing an open tubular neighborhood of  from
from  .
.  drilled along
drilled along  is also known as the link complement, since if one removed the corresponding closed tubular neighborhood from
is also known as the link complement, since if one removed the corresponding closed tubular neighborhood from  one obtains a manifold diffeomorphic to
one obtains a manifold diffeomorphic to 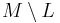 .
.
- Given a 3-manifold with torus boundary components, we may glue in a solid torus by a homeomorphism (resp. diffeomorphism) of its boundary to the torus boundary component
 of the original 3-manifold. There are many inequivalent ways of doing this, in general. This process is called Dehn filling.
of the original 3-manifold. There are many inequivalent ways of doing this, in general. This process is called Dehn filling.
- Dehn surgery on a 3-manifold containing a link consists of drilling out a tubular neighbourhood of the link together with Dehn filling on all the components of the boundary corresponding to the link.
We can pick two oriented simple closed curves m and ℓ on the boundary torus of the 3-manifold that generate the fundamental group of the torus. This gives any simple closed curve  on that torus two coordinates p and q, each coordinate corresponding to the algebraic intersection of the curve with m and ℓ respectively. These coordinates only depend on the homotopy class of
on that torus two coordinates p and q, each coordinate corresponding to the algebraic intersection of the curve with m and ℓ respectively. These coordinates only depend on the homotopy class of  .
.
We can specify a homeomorphism of the boundary of a solid torus to T by having the meridian curve of the solid torus map to a curve homotopic to  . As long as the meridian maps to the surgery slope
. As long as the meridian maps to the surgery slope ![[\gamma]](/2012-wikipedia_en_all_nopic_01_2012/I/0af9538e5a6a88e7d99837db0508aaa0.png) , the resulting Dehn surgery will yield a 3-manifold that will not depend on the specific gluing (up to homeomorphism). The ratio p/q is called the surgery coefficient.
, the resulting Dehn surgery will yield a 3-manifold that will not depend on the specific gluing (up to homeomorphism). The ratio p/q is called the surgery coefficient.
In the case of links in the 3-sphere or more generally an oriented homology sphere, there is a canonical choice of the meridians and longitudes of T. The longitude is chosen so that it is null-homologous in the knot complement—equivalently, if it is the boundary of a Seifert surface. The meridian is the curve that bounds a disc in the tubular neighbourhood of the link. When the ratios p/q are all integers, the surgery is called an integral surgery or a genuine surgery, since such surgeries are closely related to handlebodies, cobordism and Morse functions.
Results
Every closed, orientable, connected 3-manifold is obtained by performing Dehn surgery on a link in the 3-sphere. This result, the Lickorish-Wallace theorem, was first proven by Wallace in 1960 and independently by Lickorish in a stronger form in 1962. Via the now well-known relation between genuine surgery and cobordism, this result is equivalent to the theorem that the oriented cobordism group of 3-manifolds is trivial, originally due to V. Rohlin in 1951.
Since orientable 3-manifolds can all be generated by suitably decorated links, one might ask how distinct surgery presentations of a given 3-manifold might be related. The answer is called the Kirby calculus.
See also
- Hyperbolic Dehn surgery
- Tubular neighborhood
- Surgery on manifolds, in the general sense, also called spherical modification.
References
- Dehn, M. (1938), "Die Gruppe der Abbildungsklassen", Acta Mathematica 69 (1): 135–206, doi:10.1007/BF02547712.
- Thom, René (1954), "Quelques propriétés globales des variétés différentiables", Commentarii Mathematici Helvetici 28: 17–86, doi:10.1007/BF02566923, MR0061823, http://retro.seals.ch/digbib/view?did=c1:389597&sdid=c1:389960
- Kirby, Rob (1978), "A calculus for framed links in S3", Inventiones Mathematicae 45 (1): 35–56, doi:10.1007/BF01406222.
- Fenn, R. P.; Rourke, C. P. (1979), "On Kirby's calculus of links", Topology 18 (1): 1–15, doi:10.1016/0040-9383(79)90010-7.
- Gompf, Robert; Stipsicz, András (1999), 4-Manifolds and Kirby Calculus, Graduate Studies in Mathematics, 20, Providence, RI: American Mathematical Society, ISBN 0-8218-0994-6.