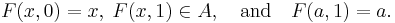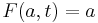Deformation retract
In topology, a branch of mathematics, a retraction [1], as the name suggests, "retracts" an entire space into a subspace. A deformation retraction is a map which captures the idea of continuously shrinking a space into a subspace.
Contents |
Definitions
Retract
Let X be a topological space and A a subspace of X. Then a continuous map
is a retraction if the restriction of r to A is the identity map on A; that is, r(a) = a for all a in A. Equivalently, denoting by
the inclusion, a retraction is a continuous map r such that
that is, the composition of r with the inclusion is the identity of A. Note that, by definition, a retraction maps X onto A. A subspace A is called a retract of X if such a retraction exists. For instance, any space retracts to a point in the obvious way (the constant map yields a retraction). If X is hausdorff, then A must be closed.
A space X is known as an absolute retract (or AR) if for every normal space Y that embeds X as a closed subset, X is a retract of Y. The unit cube In as well as the Hilbert cube Iω are absolute retracts.
Neighborhood retract
If there exists an open set U such that
and A is a retract of U, then A is called a neighborhood retract of X.
A space X is an absolute neighborhood retract (or ANR) if for every normal space Y that embeds X as a closed subset, X is a neighborhood retract of Y. The n-sphere Sn is an absolute neighborhood retract.
Deformation retract and strong deformation retract
A continuous map
is a deformation retraction of a space X onto a subspace A if, for every x in X and a in A,
In other words, a deformation retraction is a homotopy between a retraction and the identity map on X. The subspace A is called a deformation retract of X. A deformation retract is a special case of homotopy equivalence.
A retract need not be a deformation retract. For instance, having a single point as a deformation retract would imply a space is path connected (in fact, it would imply contractibility of the space).
Note: An equivalent definition of deformation retraction is the following. A continuous map r: X → A is a deformation retraction if it is a retraction and its composition with the inclusion is homotopic to the identity map on X. In this formulation, a deformation retraction carries with it a homotopy between the identity map on X and itself.
If, in the definition of a deformation retraction, we add the requirement that
for all t in [0, 1], F is called a strong deformation retraction. In other words, a strong deformation retraction leaves points in A fixed throughout the homotopy. (Some authors, such as Allen Hatcher, take this as the definition of deformation retraction.)
Neighborhood deformation retract
A pair 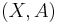 of spaces in U is an NDR-pair if there exists a map
of spaces in U is an NDR-pair if there exists a map 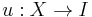 such that
such that 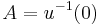 and a homotopy
and a homotopy 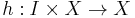 such that
such that 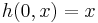 for all
for all 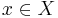 ,
, 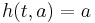 for all
for all 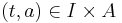 , and
, and 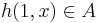 for all
for all 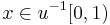 . The pair
. The pair 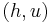 is said to be a representation of
is said to be a representation of 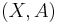 as an NDR-pair.
as an NDR-pair.
Properties
Deformation retraction is a particular case of homotopy equivalence. In fact, two spaces are homotopy equivalent if and only if they are both deformation retracts of a single larger space.
Any topological space which deformation retracts to a point is contractible. Contractibility, however, is a weaker condition, as contractible spaces exist which do not deformation retract to a point [2].
Notes
- ^ K. Borsuk (1931). "Sur les rétractes". Fund. Math. 17: 2–20.
- ^ Hatcher, Allen (2002), Algebraic topology, Cambridge University Press, ISBN 978-0-521-79540-1, http://www.math.cornell.edu/~hatcher/AT/ATpage.html
External links
- This article incorporates material from Neighborhood retract on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.
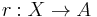
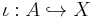
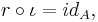
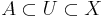
![F:X \times [0, 1] \to X \,](/2012-wikipedia_en_all_nopic_01_2012/I/e8160f3e767503fd2d836a2c86d0a8a2.png)