Defocus aberration
| Optical aberration |
|---|
DistortionSpherical aberration |
In optics, defocus is the aberration in which an image is simply out of focus. This aberration is familiar to anyone who has used a camera, videocamera, microscope, telescope, or binoculars. Optically, defocus refers to a translation along the optical axis away from the plane or surface of best focus. In general, defocus reduces the sharpness and contrast of the image. What should be sharp, high-contrast edges in a scene become gradual transitions. Fine detail in the scene is blurred or even becomes invisible. Nearly all image-forming optical devices incorporate some form of focus adjustment to minimize defocus and maximize image quality.
The degree of image blurring for a given amount of focus shift depends inversely on the lens f-number. Low f-numbers, such as f/1.4 to f/2.8, are very sensitive to defocus and have very shallow depths of focus. High f-numbers, in the f/16 to f/32 range, are highly tolerant of defocus, and consequently have large depths of focus. The limiting case in f-number is the pinhole camera, operating at perhaps f/100 to f/1000, in which case all objects are in focus almost regardless of their distance from the pinhole aperture. The penalty for achieving this extreme depth of focus is very dim illumination at the imaging film or sensor, limited resolution due to diffraction, and very long exposure time, which introduces the potential for image degradation due to motion blur.
The amount of allowable defocus is related to the resolution of the imaging medium. A lower-resolution imaging chip or film is more tolerant of defocus and other aberrations. To take full advantage of a higher resolution medium, defocus and other aberrations must be minimized.
Defocus is modeled in Zernike polynomial format as 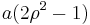 , where
, where  is the defocus coefficient in wavelengths of light. This corresponds to the parabola-shaped optical path difference between two spherical wavefronts that are tangent at their vertices and have different radii of curvature.
is the defocus coefficient in wavelengths of light. This corresponds to the parabola-shaped optical path difference between two spherical wavefronts that are tangent at their vertices and have different radii of curvature.
For some applications, such as phase contrast electron microscopy, defocused images can contain useful information. Multiple images recorded with various values of defocus can be used to examine how the intensity of a the electron wave varies in three dimensional space, and from this information the phase of the wave can be inferred. This is the basis of non-interferometric phase retrieval. Examples of phase retrieval algorithms that utilise defocused images include the Gerchberg-Saxton algorithm and various methods based on the transport of intensity equation.
See also
References
- Smith, Warren J., Modern Optical Engineering, McGraw-Hill, 2000, Chapter 11, ISBN 0-07-136360-2