Deductive closure
Peter D. Klein, in the second edition of The Cambridge Dictionary of Philosophy, defines closure as follows:
A set of objects, O, is said to exhibit closure or to be closed under a given operation, R, provided that for every object, x, if x is a member of O and x is R-related to any object, y, then y is a member of O. [links not in original]
In propositional logic, the set of all propositions exhibits deductive closure: if set O is the set of propositions, and operation R is logical entailment (“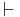 ”), then provided that proposition p is a member of O and p is R-related to q (i.e., p
”), then provided that proposition p is a member of O and p is R-related to q (i.e., p 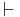 q), q is also a member of O. In the philosophical branch of epistemology, many philosophers have and continue to debate whether particular subsets of propositions—especially ones ascribing knowledge or justification of a belief to a subject—are closed under deduction.
q), q is also a member of O. In the philosophical branch of epistemology, many philosophers have and continue to debate whether particular subsets of propositions—especially ones ascribing knowledge or justification of a belief to a subject—are closed under deduction.
Epistemic closure
It is not the case that knowledge is closed under deduction; that is, if person S knows p, and p entails q, then S knows q (sometimes called the straight principle). [1] A subject may not actually believe q, for example, regardless of whether he or she is justified or warranted. Thus, one might instead say that knowledge is closed under known deduction: if, while knowing p, S believes q because S knows that p entails q, then S knows q.[1] An even stronger formulation would be as such: If, while knowing various propositions, S believes p because S knows that they entail p, then S knows p.[1] While the principle of epistemic closure is generally regarded as intuitive,[2] philosophers such as Robert Nozick and Fred Dretske have argued against it.
Justificatory closure
In the seminal 1963 paper, “Is Justified True Belief Knowledge?”, Edmund Gettier gave an assumption (later called the “principle of deducibility for justification” by Irving Thalberg Jr.[3]) that would serve as a basis for the rest of his piece: “for any proposition P, if S is justified in believing P and P entails Q, and S deduces Q from P and accepts Q as a result of this deduction, then S is justified in believing Q.”[4] This was seized upon by Thalberg, who rejected the principle in order to demonstrate that one of Gettier's examples fails to support Gettier's main thesis that justified true belief is not knowledge (in the following quotation, (1) refers to “Jones will get the job”, (2) refers to “Jones has ten coins”, and (3) is the logical conjunction of (1) and (2)):
Why doesn't Gettier's principle (PDJ) hold in the evidential situation he has described? You multiply your risks of being wrong when you believe a conjunction. [… T]he most elementary theory of probability indicates that Smith's prospects of being right on both (1) and (2), namely, of being right on (3), are bound to be less favorable than his prospects of being right on either (1) or (2). In fact, Smith's chances of being right on (3) might not come up to the minimum standard of justification which (1) and (2) barely satisfy, and Smith would be unjustified in accepting (3). [Thalberg p. 798]
References
- ^ a b c Luper, Steven. “The Epistemic Closure Principle.” Stanford Encyclopedia of Philosophy. Dec 31, 2001. http://plato.stanford.edu/entries/closure-epistemic/#CloPri (accessed November 2, 2006).
- ^ Brady, Michael, and Duncan Pritchard. “Epistemological Contextualism: Problems and Prospects.” The Philosophical Quarterly 55, no. 219 (2005): 161–171.
- ^ Thalberg Jr., Irving. “In Defense of Justified True Belief.” Journal of Philosophy, 66, no. 22 (1969): 794–803.
- ^ Gettier, Edmund. “Is Justified True Belief Knowledge?” Analysis, 23, no. 6 (1963): 121–123.