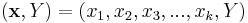Decision tree learning
Decision tree learning, used in statistics, data mining and machine learning, uses a decision tree as a predictive model which maps observations about an item to conclusions about the item's target value. More descriptive names for such tree models are classification trees or regression trees. In these tree structures, leaves represent class labels and branches represent conjunctions of features that lead to those class labels.
In decision analysis, a decision tree can be used to visually and explicitly represent decisions and decision making. In data mining, a decision tree describes data but not decisions; rather the resulting classification tree can be an input for decision making. This page deals with decision trees in data mining.
Contents |
General
Decision tree learning is a method commonly used in data mining. The goal is to create a model that predicts the value of a target variable based on several input variables. An example is shown on the right. Each interior node corresponds to one of the input variables; there are edges to children for each of the possible values of that input variable. Each leaf represents a value of the target variable given the values of the input variables represented by the path from the root to the leaf.
A tree can be "learned" by splitting the source set into subsets based on an attribute value test. This process is repeated on each derived subset in a recursive manner called recursive partitioning. The recursion is completed when the subset at a node all has the same value of the target variable, or when splitting no longer adds value to the predictions.
In data mining, decision trees can be described also as the combination of mathematical and computational techniques to aid the description, categorisation and generalisation of a given set of data.
Data comes in records of the form:
The dependent variable, Y, is the target variable that we are trying to understand, classify or generalise. The vector x is composed of the input variables, x1, x2, x3 etc., that are used for that task.
Types
Decision trees used in data mining are of two main types:
- Classification tree analysis is when the predicted outcome is the class to which the data belongs.
- Regression tree analysis is when the predicted outcome can be considered a real number (e.g. the price of a house, or a patient’s length of stay in a hospital).
The term Classification And Regression Tree (CART) analysis is an umbrella term used to refer to both of the above procedures, first introduced by Breiman et al.[1] Trees used for regression and trees used for classification have some similarities - but also some differences, such as the procedure used to determine where to split.[1]
Some techniques use more than one decision tree for their analysis:
- A Random Forest classifier uses a number of decision trees, in order to improve the classification rate.
- Boosted Trees can be used for regression-type and classification-type problems.[2][3]
- Rotation forest - in which every decision tree is trained by first applying principal component analysis (PCA) on a random subset of the input features. [4]
There are many specific decision-tree algorithms. Notable ones include:
- ID3 algorithm
- C4.5 algorithm
- CHi-squared Automatic Interaction Detector (CHAID). Performs multi-level splits when computing classification trees.[5]
- MARS: extends decision trees to better handle numerical data
Formulae
The algorithms that are used for constructing decision trees usually work top-down by choosing a variable at each step that is the next best variable to use in splitting the set of items.[6] "Best" is defined by how well the variable splits the set into homogeneous subsets that have the same value of the target variable. Different algorithms use different formulae for measuring "best". This section presents a few of the most common formulae. These formulae are applied to each candidate subset, and the resulting values are combined (e.g., averaged) to provide a measure of the quality of the split.
Gini impurity
Used by the CART algorithm, Gini impurity is a measure of how often a randomly chosen element from the set would be incorrectly labeled if it were randomly labeled according to the distribution of labels in the subset. Gini impurity can be computed by summing the probability of each item being chosen times the probability of a mistake in categorizing that item. It reaches its minimum (zero) when all cases in the node fall into a single target category.
To compute Gini impurity for a set of items, suppose y takes on values in {1, 2, ..., m}, and let fi = the fraction of items labeled with value i in the set.
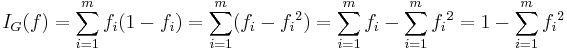
Information gain
Used by the ID3, C4.5 and C5.0 tree generation algorithms. Information gain is based on the concept of entropy used in information theory.
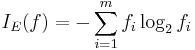
Decision tree advantages
Amongst other data mining methods, decision trees have various advantages:
- Simple to understand and interpret. People are able to understand decision tree models after a brief explanation.
- Requires little data preparation. Other techniques often require data normalisation, dummy variables need to be created and blank values to be removed.
- Able to handle both numerical and categorical data. Other techniques are usually specialised in analysing datasets that have only one type of variable. Ex: relation rules can be used only with nominal variables while neural networks can be used only with numerical variables.
- Uses a white box model. If a given situation is observable in a model the explanation for the condition is easily explained by boolean logic. An example of a black box model is an artificial neural network since the explanation for the results is difficult to understand.
- Possible to validate a model using statistical tests. That makes it possible to account for the reliability of the model.
- Robust. Performs well even if its assumptions are somewhat violated by the true model from which the data were generated.
- Performs well with large data in a short time. Large amounts of data can be analysed using standard computing resources.
Limitations
- The problem of learning an optimal decision tree is known to be NP-complete under several aspects of optimality and even for simple concepts.[7][8] Consequently, practical decision-tree learning algorithms are based on heuristic algorithms such as the greedy algorithm where locally optimal decisions are made at each node. Such algorithms cannot guarantee to return the globally optimal decision tree.
- Decision-tree learners can create over-complex trees that do not generalise the data well. This is called overfitting.[9] Mechanisms such as pruning are necessary to avoid this problem.
- There are concepts that are hard to learn because decision trees do not express them easily, such as XOR, parity or multiplexer problems. In such cases, the decision tree becomes prohibitively large. Approaches to solve the problem involve either changing the representation of the problem domain (known as propositionalisation)[10] or using learning algorithms based on more expressive representations (such as statistical relational learning or inductive logic programming).
- For data including categorical variables with different number of levels, information gain in decision trees are biased in favor of those attributes with more levels.[11]
Extensions
Decision graphs
In a decision tree, all paths from the root node to the leaf node proceed by way of conjunction, or AND. In a decision graph, it is possible to use disjunctions (ORs) to join two more paths together using Minimum Message Length (MML).[12] Decision graphs have been further extended to allow for previously unstated new attributes to be learnt dynamically and used at different places within the graph.[13] The more general coding scheme results in better predictive accuracy and log-loss probabilistic scoring. In general, decision graphs infer models with fewer leaves than decision trees.
Search through Evolutionary Algorithms
Evolutionary algorithms have been used to avoid local optimal decisions and search the decision tree space with little a priori bias.[14] [15]
See also
- Decision tree pruning
- Binary decision diagram
- CART
- Decision stump
- Incremental decision tree
- Alternating decision tree
- Structured data analysis (statistics)
Implementations
- Weka, a free and open-source data mining suite, contains many decision tree algorithms
- Orange, a free data mining software suite, module orngTree
- KNIME
References
- ^ a b Breiman, Leo; Friedman, J. H., Olshen, R. A., & Stone, C. J. (1984). Classification and regression trees. Monterey, CA: Wadsworth & Brooks/Cole Advanced Books & Software. ISBN 978-0412048418.
- ^ Friedman, J. H. (1999). Stochastic gradient boosting. Stanford University.
- ^ Hastie, T., Tibshirani, R., Friedman, J. H. (2001). The elements of statistical learning : Data mining, inference, and prediction. New York: Springer Verlag.
- ^ Rodriguez, J.J. and Kuncheva, L.I. and Alonso, C.J. (2006), Rotation forest: A new classifier ensemble method, IEEE Transactions on Pattern Analysis and Machine Intelligence, 28(10):1619-1630.
- ^ Kass, G. V. (1980). "An exploratory technique for investigating large quantities of categorical data". Applied Statistics 29 (2): 119–127. doi:10.2307/2986296. JSTOR 2986296.
- ^ Rokach, L.; Maimon, O. (2005). "Top-down induction of decision trees classifiers-a survey". IEEE Transactions on Systems, Man, and Cybernetics, Part C 35 (4): 476–487. doi:10.1109/TSMCC.2004.843247.
- ^ Hyafil, Laurent; Rivest, RL (1976). "Constructing Optimal Binary Decision Trees is NP-complete". Information Processing Letters 5 (1): 15–17. doi:10.1016/0020-0190(76)90095-8.
- ^ Murthy S. (1998). Automatic construction of decision trees from data: A multidisciplinary survey. Data Mining and Knowledge Discovery
- ^ Principles of Data Mining. 2007. doi:10.1007/978-1-84628-766-4. ISBN 978-1-84628-765-7.
- ^ Horváth, Tamás; Yamamoto, Akihiro, eds (2003). Inductive Logic Programming. Lecture Notes in Computer Science. 2835. doi:10.1007/b13700. ISBN 978-3-540-20144-1.
- ^ Deng,H.; Runger, G.; Tuv, E. (2011). "Bias of importance measures for multi-valued attributes and solutions". Proceedings of the 21st International Conference on Artificial Neural Networks (ICANN). pp. 293–300. http://enpub.fulton.asu.edu/hdeng3/MultiICANN2011.pdf.
- ^ http://citeseer.ist.psu.edu/oliver93decision.html
- ^ Tan & Dowe (2003)
- ^ Papagelis A., Kalles D.(2001). Breeding Decision Trees Using Evolutionary Techniques, Proceedings of the Eighteenth International Conference on Machine Learning, p.393-400, June 28-July 01, 2001
- ^ Barros, Rodrigo C., Basgalupp, M. P., Carvalho, A. C. P. L. F., Freitas, Alex A. (2011). A Survey of Evolutionary Algorithms for Decision-Tree Induction. IEEE Transactions on Systems, Man and Cybernetics, Part C: Applications and Reviews
External links
- Building Decision Trees in Python From O'Reilly.
- An Addendum to "Building Decision Trees in Python" From O'Reilly.
- Decision Trees page at aaai.org, a page with commented links.
- Decision tree implementation in Ruby (AI4R)