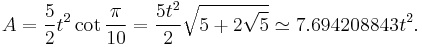Decagon

Regular decagon
Edges and vertices 10
Schläfli symbol {10}
t{5}
Coxeter–Dynkin diagrams
Symmetry group Dihedral (D10)
Internal angle (degrees) 144°
Properties convex, cyclic, equilateral, isogonal, isotoxal

In geometry, a decagon is any polygon with ten sides and ten angles, and usually refers to a regular decagon, having all sides of equal length and each internal angle equal to 144°. Its Schläfli symbol is {10}.

Contents

Regular decagon

The area of a regular decagon is: (with t = edge length)

A = \frac{5}{2}t^2 \cot \frac{\pi}{10} = \frac{5t^2}{2} \sqrt{5%2B2\sqrt{5}} \simeq 7.694208843 t^2.

An alternative formula is 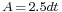\scriptstyle A\,=\,2.5dt where d is the distance between parallel sides, or the height when the decagon stands on one side as base.
By simple trigonometry 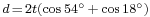\scriptstyle d\,=\,2t(\cos{54^\circ}\,%2B\,\cos{18^\circ}).

Sides

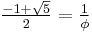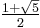The side of a regular decagon inscribed in a unit circle is \tfrac{-1%2B\sqrt{5}}{2}=\tfrac{1}{\phi}, where ϕ is the golden ratio, \tfrac{1%2B\sqrt{5}}{2}.

Construction

A regular decagon is constructible using compass and straightedge:

An alternative (but similar) method is as follows:

  1. Construct a pentagon in a circle by one of the methods shown in constructing a pentagon.
  2. Extend a line from each vertex of the pentagon through the center of the circle to the opposite side of that same circle. Where each line cuts the circle is a vertex of the decagon.
  3. The five corners of the pentagon constitute alternate corners of the decagon. Join these points to the adjacent new points to form the decagon.

Related figures

There is one regular star polygon, the decagram {10/3}, using the same points, but connecting every third points. There are also two compounds: {10/4} is reduced to 2{5/2} as two pentagrams, and {10/2} is reduced to 2{5} as two pentagons.


{10/3}
Decagram
{10/2} or 2{5}
{10/4} or 2{5/2}

Petrie polygons

The regular decagon is the Petrie polygon for many higher dimensional polytopes, shown in these skew orthogonal projections in various Coxeter planes:

A9
9-simplex
Rectified 9-simplex
Trirectified 9-simplex
Quadrirectified 9-simplex
Quintirectified 9-simplex
BC5
5-orthoplex
Rectified 5-orthoplex
Birectified 5-cube
Rectified 5-cube
5-cube
D6
t1(431)
t3(131)
t2(131)
t1(131)
6-demicube
(131)
H3
Dodecahedron
Icosahedron
Icosidodecahedron

See also

External links

Listed by number of sides
1–10 sides
11–20 sides
Others
Star polygons