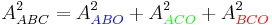De Gua's theorem
De Gua's theorem is a three-dimensional analog of the Pythagorean theorem and named for Jean Paul de Gua de Malves.
If a tetrahedron has a right-angle corner (like the corner of a cube), then the square of the area of the face opposite the right-angle corner is the sum of the squares of the areas of the other three faces.
The Pythagorean theorem and de Gua's theorem are special cases (n = 2, 3) of a general theorem about n-simplices with a right angle corner.
Jean Paul de Gua de Malves (1713-1785) published the theorem in 1783, but around the same time a slightly more general version was published by another French mathematician, Tinseau d'Amondans (1746-1818), as well. However the theorem had been known much earlier to Johann Faulhaber (1580-1635) and René Descartes (1596-1650).[1][2]
Notes
- ^ Weisstein, Eric W., "de Gua's theorem" from MathWorld.
- ^ Hans-Bert Knoop: Ausgewählte Kapitel zur Geschichte der Mathematik. Lecture Notes (University of Düsseldorf), p. 55 (§ 4 Pythagoreische n-Tupel, p. 50-65) (German)
References
- Weisstein, Eric W., "de Gua's theorem" from MathWorld.
- Sergio A. Alvarez: Note on an n-dimensional Pythagorean theorem, Carnegie Mellon University
- De Gua's Theorem, Pythagorean theorem in 3-D - graphical illustration and related properties of the tetrahedron