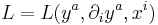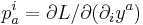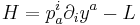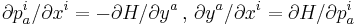De Donder–Weyl theory
The De Donder–Weyl theory is a formalism in the calculus of variations over spacetime which treats the space and time coordinates on equal footing. In this framework, a field is represented as a system that varies both in space and in time.
| De Donder–Weyl equations: |
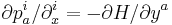 |
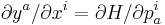 |
Contents |
De Donder–Weyl formulation of field theory
The De Donder–Weyl theory is based on a change of variables. Let 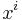 be spacetime coordinates, for i=1 to n (with n=4 representing 3+1 dimensions of space and time), and
be spacetime coordinates, for i=1 to n (with n=4 representing 3+1 dimensions of space and time), and 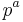 field variables, for a=1 to m, and
field variables, for a=1 to m, and  the Lagrangian density.
the Lagrangian density.
With polymomenta 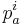 defined as
defined as
and for De Donder–Weyl Hamiltonian function  defined as
defined as
the De Donder–Weyl equations are:[1]
These canonical equations of motion are covariant. The theory is a formulation of a covariant Hamiltonian field theory and for n=1 it reduces to Hamiltonian mechanics (see also action principle in the calculus of variations).
History
The formalism, now known as De Donder–Weyl (DW) theory, was developed by Hermann Weyl and, independently, by Théophile de Donder.[2] Weyl's made his proposal in 1934, inspired by work of Constantin Carathéodory which in turn was founded on the work of Vito Volterra. The work of De Donder in contrast started from the theory of integral invariants.[3] The De Donder–Weyl theory has thus known in the calculus of variations since the 1930s, and initially found only rare application in physics. It has recently found increased interest in theoretical physics in relation to quantum field theory.[4]
In 1970, Jedrzej Śniatycki, author of book on Geometric quantization and quantum mechanics, developed an invariant geometrical formulation of jet bundles building on the work of De Donder and Weyl.[5] Theoretical physicist Igor V. Kanatchikov showed in 1999 that the De Donder–Weyl covariant Hamiltonian field equations can be formulated in terms of Duffin–Kemmer–Petiau matrices.[6]
Further reading
- Cornelius Paufler, Hartmann Römer: De Donder–Weyl equations and multisymplectic geometry, Reports on Mathematical Physics, vol. 49 (2002), no. 2–3, pp. 325–334
- Krzysztof Maurin: The Riemann legacy: Riemannian ideas in mathematics and physics, Part II, Chapter 7.16 Field theories for calculus of variation for multiple integrals, Kluwer Academic Publishers, ISBN 0-7923-4636-X, 1997, p. 482 ff.
References
- ^ Igor V. Kanatchikov: Towards the Born–Weyl quantization of fields, arXiv:quant-ph/9712058v1 (submitted on 31 December 1997)
- ^ Frédéric Hélein: Hamiltonian formalisms for multidimensional calculus of variations and perturbation theory. In Haïm Brézis, Felix E. Browder, Abbas Bahri, Sergiu Klainerman, Michael Vogelius (ads.): Noncompact problems at the intersection of geometry, analysis, and topology, American Mathematical Society, 2004, pp. 127–148, p. 131, ISBN 0-8218-3635-8,
- ^ Roger Bielawski,Kevin Houston, Martin Speight: Variational Problems in Differential Geometry, London Mathematical Society Lecure Notes Series, no. 394, University of Leeds, 2009, ISBN 978-0-521-28274-1, p. 104 f.
- ^ Igor V. Kanatchikov: De Donder–Weyl theory and a hypercomplex extension of quantum mechanics to field theory, arXiv:hep-th/9810165v1 (submitted on 21 October 1998)
- ^ Jedrzej Śniatycki, 1970. Cited after: Yvette Kosmann-Schwarzbach: The Noether Theorems: Invariance and Conservation Laws in the 20th Century, Springer, 2011, ISBN 978-0-387-87867-6, p. 111
- ^ Igor V. Kanatchikov: On the Duffin–Kemmer–Petiau formulation of the covariant Hamiltonian dynamics in field theory, arXiv:hep-th/9911/9911175v1 (submitted on 23 November 1999)