Complete partial order

In mathematics, directed complete partial orders and ω-complete partial orders (abbreviated to dcpo, ωcpo or sometimes just cpo) are special classes of partially ordered sets, characterized by particular completeness properties. Complete partial orders play a central role in theoretical computer science, in denotational semantics and domain theory.

Contents 1 Definitions 2 Examples 3 Properties 4 Continuous functions and fixpoints 5 See also 6 Notes 7 References

Definitions

A partially ordered set is a directed complete partial order (dcpo) if each of its directed subsets has a supremum. Recall that a subset of a partial order is directed if it is non-empty and every pair of elements has an upper bound in the set. In the literature, dcpos sometimes also appear under the label up-complete poset or simply cpo.

In some contexts, the phrase ω-cpo (or just cpo) is used to describe a poset in which every ω-chain (x₁≤x₂≤x₃≤x₄≤...) has a supremum. Every dcpo is an ω-cpo.

An important role is played by dcpo's with a least element. They are sometimes called pointed dcpos, or cppos, or just cpos.

Requiring the existence of directed suprema can be motivated by viewing directed sets as generalized approximation sequences and suprema as limits of the respective (approximative) computations. This intuition, in the context of denotational semantics, was the motivation behind the development of domain theory.

The dual notion of a directed complete poset is called a filtered complete partial order. However, this concept occurs far less frequently in practice, since one usually can work on the dual order explicitly.

Examples

• Every finite poset is directed complete.
• All complete lattices are also directed complete.
• For any poset, the set of all non-empty filters, ordered by subset inclusion, is a dcpo. Together with the empty filter it is also pointed. If the order has binary meets, then this construction (including the empty filter) actually yields a complete lattice.
• The set of all partial functions on some given set S can be ordered by defining f ≤ g for functions f and g if and only if g extends f, i.e. if the domain of f is a subset of the domain of g and the values of f and g agree on all inputs for which both functions are defined. (Equivalently, f ≤ g if and only if f ⊆ g where f and g are identified with their respective graphs.) This order is a pointed dcpo, where the least element is the nowhere defined function (with empty domain). In fact, ≤ is also bounded complete. This example also demonstrates why it is not always natural to have a greatest element.
• The specialization order of any sober space is a dcpo.
• Let us use the term “deductive system” as a set of sentences closed under consequence (for defining notion of consequence, let us use e.g. Tarski's algebraic approach^[1][2]). There are interesting theorems which concern a set of deductive systems being a directed complete partial ordering.^[3] Also, a set of deductive systems can be chosen to have a least element in a natural way (so that it can be also a complete partial ordering), because the set of all consequences of the empty set (i.e. “the set of the logically provable / logically valid sentences”) is (1) a deductive system (2) contained by all deductive systems.

Properties

An ordered set P is a pointed dcpo if and only if every chain has a supremum in P. Alternatively, an ordered set P is a pointed dcpo if and only if every order-preserving self-map of P has a least fixpoint. Every set S can be turned into a pointed dcpo by adding a least element ⊥ and introducing a flat order with ⊥ ≤ s and s ≤ s for every s ∈ S and no other order relations.

Continuous functions and fixpoints

A function f between two dcpos P and Q is called (Scott) continuous if it maps directed sets to directed sets while preserving their suprema:

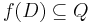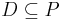• is directed for every directed .
• for every directed .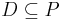

Note that every continuous function between dcpos is a monotone function. This notion of continuity is equivalent to the topological continuity induced by the Scott topology.

The set of all continuous functions between two dcpos P and Q is denoted [P → Q]. Equipped with the pointwise order, this is again a dcpo, and a cpo whenever Q is a cpo. Thus the complete partial orders with Scott continuous maps form a cartesian closed category.^[4]

Every order-preserving self-map f of a cpo (P, ⊥) has a least fixpoint.^[5] If f is continuous then this fixpoint is equal to the supremum of the iterates (⊥, f(⊥), f(f(⊥)), … fⁿ(⊥), …) of ⊥ (see also the Kleene fixpoint theorem).

See also

Directed completeness relates in various ways to other completeness notions. Directed completeness alone is quite a basic property that occurs often in other order theoretic investigations, using for instance algebraic posets and the Scott topology.

Notes

1. ^ Tarski, Alfred: Bizonyítás és igazság / Válogatott tanulmányok. Gondolat, Budapest, 1990. (Title means: Proof and truth / Selected papers.)
2. ^ Stanley N. Burris and H.P. Sankappanavar: A Course in Universal Algebra
3. ^ See online in p. 24 exercises 5–6 of §5 in BurSan:UnivAlg. Or, on paper, see Tar:BizIg.
4. ^ Barendregt, Henk, The lambda calculus, its syntax and semantics, North-Holland (1984)
5. ^ See Knaster–Tarski theorem; The foundations of program verification, 2nd edition, Jacques Loeckx and Kurt Sieber, John Wiley & Sons, ISBN 0-471-91282-4, Chapter 4; the Knaster-Tarski theorem, formulated over cpo's, is given to prove as exercise 4.3-5 on page 90.

References

• Davey, B.A., and Priestley, H. A. (2002). Introduction to Lattices and Order (Second ed.). Cambridge University Press. ISBN 0-521-78451-4.