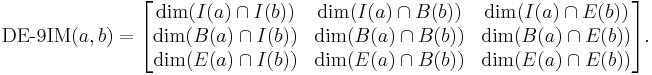DE-9IM

In geometry, a dimensionally extended nine-intersection model (DE-9IM) is a topological model used to describe the spatial relation of two geometries in two-dimensions (R2). The representation was developed by Clementini and others[1][2] and is used as a basis for spatial predicate functions in geographic information systems (GIS) and spatial databases.

The DE-9IM model is based on a 3×3 intersection matrix with the form:

\operatorname{DE-9IM}(a,b) = \begin{bmatrix} \dim(I(a) \cap I(b)) & \dim(I(a) \cap B(b)) & \dim(I(a) \cap E(b)) \\ \dim(B(a) \cap I(b)) & \dim(B(a) \cap B(b)) & \dim(B(a) \cap E(b))\\ \dim(E(a) \cap I(b)) & \dim(E(a) \cap B(b)) & \dim(E(a) \cap E(b)) \end{bmatrix}.

where dim is the maximum number of dimensions of the intersection (∩) of the interior (I), boundary (B), and exterior (E) of geometries a and b. Empty sets (∅) are denoted as −1 or F (false). Non-empty sets (¬∅) or T (true) are denoted with the maximum number of dimensions of the intersection, specifically 0 for points, 1 for lines, 2 for areas. The domain of the model also uses * as a wildcard for any condition for dim. The matrix can be represented in a single-line string pattern.

The spatial predicate functions that can be derived from DE-9IM include:[3]

Name (synonym) Intersection matrix and code string
Equals \Bigl[\begin{smallmatrix} \mathrm{T}&\mathrm{*}&\mathrm{F}\\ \mathrm{*}&\mathrm{*}&\mathrm{F}\\ \mathrm{F}&\mathrm{F}&\mathrm{*} \end{smallmatrix}\Bigr]
T*F**FFF*
Disjoint \Bigl[\begin{smallmatrix} \mathrm{F}&\mathrm{F}&\mathrm{*}\\ \mathrm{F}&\mathrm{F}&\mathrm{*}\\ \mathrm{*}&\mathrm{*}&\mathrm{*} \end{smallmatrix}\Bigr]
FF*FF****
Intersects \Bigl[\begin{smallmatrix} \mathrm{T}&\mathrm{*}&\mathrm{*}\\ \mathrm{*}&\mathrm{*}&\mathrm{*}\\ \mathrm{*}&\mathrm{*}&\mathrm{*} \end{smallmatrix}\Bigr] or \Bigl[\begin{smallmatrix} \mathrm{*}&\mathrm{T}&\mathrm{*}\\ \mathrm{*}&\mathrm{*}&\mathrm{*}\\ \mathrm{*}&\mathrm{*}&\mathrm{*} \end{smallmatrix}\Bigr] or \Bigl[\begin{smallmatrix} \mathrm{*}&\mathrm{*}&\mathrm{*}\\ \mathrm{T}&\mathrm{*}&\mathrm{*}\\ \mathrm{*}&\mathrm{*}&\mathrm{*} \end{smallmatrix}\Bigr] or \Bigl[\begin{smallmatrix} \mathrm{*}&\mathrm{*}&\mathrm{*}\\ \mathrm{*}&\mathrm{T}&\mathrm{*}\\ \mathrm{*}&\mathrm{*}&\mathrm{*} \end{smallmatrix}\Bigr]
T******** *T******* ***T***** ****T****
Touches (meets) \Bigl[\begin{smallmatrix} \mathrm{F}&\mathrm{T}&\mathrm{*}\\ \mathrm{*}&\mathrm{*}&\mathrm{*}\\ \mathrm{*}&\mathrm{*}&\mathrm{*} \end{smallmatrix}\Bigr] or \Bigl[\begin{smallmatrix} \mathrm{F}&\mathrm{*}&\mathrm{*}\\ \mathrm{T}&\mathrm{*}&\mathrm{*}\\ \mathrm{*}&\mathrm{*}&\mathrm{*} \end{smallmatrix}\Bigr] or \Bigl[\begin{smallmatrix} \mathrm{F}&\mathrm{*}&\mathrm{*}\\ \mathrm{*}&\mathrm{T}&\mathrm{*}\\ \mathrm{*}&\mathrm{*}&\mathrm{*} \end{smallmatrix}\Bigr]
FT******* F**T***** F***T****
Crosses \Bigl[\begin{smallmatrix} \mathrm{T}&\mathrm{*}&\mathrm{T}\\ \mathrm{*}&\mathrm{*}&\mathrm{*}\\ \mathrm{*}&\mathrm{*}&\mathrm{*} \end{smallmatrix}\Bigr] or \Bigl[\begin{smallmatrix} \mathrm{T}&\mathrm{*}&\mathrm{*}\\ \mathrm{*}&\mathrm{*}&\mathrm{*}\\ \mathrm{T}&\mathrm{*}&\mathrm{*} \end{smallmatrix}\Bigr] or \Bigl[\begin{smallmatrix} \mathrm{0}&\mathrm{*}&\mathrm{*}\\ \mathrm{*}&\mathrm{*}&\mathrm{*}\\ \mathrm{*}&\mathrm{*}&\mathrm{*} \end{smallmatrix}\Bigr]
T*T****** T*****T** 0********
Within (inside) \Bigl[\begin{smallmatrix} \mathrm{T}&\mathrm{*}&\mathrm{F}\\ \mathrm{*}&\mathrm{*}&\mathrm{F}\\ \mathrm{*}&\mathrm{*}&\mathrm{*} \end{smallmatrix}\Bigr]
T*F**F***
Contains \Bigl[\begin{smallmatrix} \mathrm{T}&\mathrm{*}&\mathrm{*}\\ \mathrm{*}&\mathrm{*}&\mathrm{*}\\ \mathrm{F}&\mathrm{F}&\mathrm{*} \end{smallmatrix}\Bigr]
T*****FF*
Overlaps \Bigl[\begin{smallmatrix} \mathrm{T}&\mathrm{*}&\mathrm{T}\\ \mathrm{*}&\mathrm{*}&\mathrm{*}\\ \mathrm{T}&\mathrm{*}&\mathrm{*} \end{smallmatrix}\Bigr] or \Bigl[\begin{smallmatrix} \mathrm{1}&\mathrm{*}&\mathrm{T}\\ \mathrm{*}&\mathrm{*}&\mathrm{*}\\ \mathrm{T}&\mathrm{*}&\mathrm{*} \end{smallmatrix}\Bigr]
T*T***T** 1*T***T**
Covers \Bigl[\begin{smallmatrix} \mathrm{T}&\mathrm{*}&\mathrm{*}\\ \mathrm{*}&\mathrm{*}&\mathrm{*}\\ \mathrm{F}&\mathrm{F}&\mathrm{*} \end{smallmatrix}\Bigr] or \Bigl[\begin{smallmatrix} \mathrm{*}&\mathrm{T}&\mathrm{*}\\ \mathrm{*}&\mathrm{*}&\mathrm{*}\\ \mathrm{F}&\mathrm{F}&\mathrm{*} \end{smallmatrix}\Bigr] or \Bigl[\begin{smallmatrix} \mathrm{*}&\mathrm{*}&\mathrm{*}\\ \mathrm{T}&\mathrm{*}&\mathrm{*}\\ \mathrm{F}&\mathrm{F}&\mathrm{*} \end{smallmatrix}\Bigr] or \Bigl[\begin{smallmatrix} \mathrm{*}&\mathrm{*}&\mathrm{*}\\ \mathrm{*}&\mathrm{T}&\mathrm{*}\\ \mathrm{F}&\mathrm{F}&\mathrm{*} \end{smallmatrix}\Bigr]
T*****FF* *T****FF* ***T**FF* ****T*FF*
CoveredBy \Bigl[\begin{smallmatrix} \mathrm{T}&\mathrm{*}&\mathrm{F}\\ \mathrm{*}&\mathrm{*}&\mathrm{F}\\ \mathrm{*}&\mathrm{*}&\mathrm{*} \end{smallmatrix}\Bigr] or \Bigl[\begin{smallmatrix} \mathrm{*}&\mathrm{T}&\mathrm{F}\\ \mathrm{*}&\mathrm{*}&\mathrm{F}\\ \mathrm{*}&\mathrm{*}&\mathrm{*} \end{smallmatrix}\Bigr] or \Bigl[\begin{smallmatrix} \mathrm{*}&\mathrm{*}&\mathrm{F}\\ \mathrm{T}&\mathrm{*}&\mathrm{F}\\ \mathrm{*}&\mathrm{*}&\mathrm{*} \end{smallmatrix}\Bigr] or \Bigl[\begin{smallmatrix} \mathrm{*}&\mathrm{*}&\mathrm{F}\\ \mathrm{*}&\mathrm{T}&\mathrm{F}\\ \mathrm{*}&\mathrm{*}&\mathrm{*} \end{smallmatrix}\Bigr]
T*F**F*** *TF**F*** **FT*F*** **F*TF***

References

  1. ^ Clementini, Eliseo; Paolino Di Felice and Peter van Oosterom (1993). "A small set of formal topological relationships suitable for end-user interaction". In Abel, David; Ooi, Beng Chin. Advances in Spatial Databases: Third International Symposium, SSD '93 Singapore, June 23–25, 1993 Proceedings. Lecture Notes in Computer Science. 692/1993. Springer. pp. 277–295. doi:10.1007/3-540-56869-7_16. 
  2. ^ Clementini, Eliseo; Sharma, Jayant; Egenhofer, Max J. (1994). "Modelling topological spatial relations: Strategies for query processing". Computers & Graphics 18 (6): 815–822. doi:10.1016/0097-8493(94)90007-8. 
  3. ^ JTS: Class IntersectionMatrix, Vivid Solutions, Inc., http://www.vividsolutions.com/jts/javadoc/com/vividsolutions/jts/geom/IntersectionMatrix.html 

External links