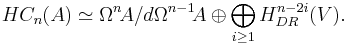Cyclic homology

In homological algebra, cyclic homology and cyclic cohomology are (co)homology theories for associative algebras introduced by Alain Connes around 1980, which play an important role in his noncommutative geometry. They were independently discovered by Boris Tsygan and studied by Connes, Karoubi, Feigin-Tsygan, Loday, Quillen, and others.

Contents

Hints about definition

The first definition of the cyclic homology of a ring A over a field of characteristic zero, denoted

HCn(A) or Hnλ(A),

proceeded by the means of an explicit chain complex related to the Hochschild homology complex of A. Connes later found a more categorical approach to cyclic homology using a notion of cyclic object in an abelian category, which is analogous to the notion of simplicial object. In this way, cyclic homology (and cohomology) may be interpreted as a derived functor, which can be explicitly computed by the means of the Connes bicomplex.

One of the striking features of cyclic homology is the existence of a long exact sequence connecting Hochschild and cyclic homology. This long exact sequence is referred to as the periodicity sequence.

Case of commutative rings

Cyclic cohomology of the commutative algebra A of regular functions on an affine algebraic variety over a field k of characteristic zero can be computed in terms of Grothendieck's algebraic de Rham complex. In particular, if the variety V=Spec A is smooth, cyclic cohomology of A are expressed in terms of the de Rham cohomology of V as follows:

HC_n(A)\simeq \Omega^n\!A/d\Omega^{n-1}\!A\oplus \bigoplus_{i\geq 1}H^{n-2i}_{DR}(V).

This formula suggests a way to define de Rham cohomology for a 'noncommutative spectrum' of a noncommutative algebra A, which was extensively developed by Connes.

Variants of cyclic homology

One motivation of cyclic homology was the need for an approximation of K-theory that be defined, unlike K-theory, as the homology of a chain complex. Cyclic cohomology is in fact endowed with a pairing with K-theory, and one hopes this pairing to be non-degenerate.

There has been defined a number of variants whose purpose is to fit better with algebras with topology, such as Fréchet algebras, 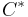C^*-algebras, etc. The reason is that K-theory behaves much better on topological algebras such as Banach algebras or C*-algebras than on algebras without additional structure. Since, on the other hand, cyclic homology degenerates on C*-algebras, there came up the need to define modified theories. Among them are entire cyclic homology due to Alain Connes, analytic cyclic homology due to Ralf Meyer or asymptotic and local cyclic homology due to Michael Puschnigg. The last one is very near to K-theory as it is endowed with a bivariant Chern character from KK-theory.

Applications

One of the applications of cyclic homology is to find new proofs and generalizations of the Atiyah-Singer index theorem. Among these generalizations are index theorems for quantum tori and quantum groups,[1] for D-modules,[2] for deformation quantization [3](Weyl quantization). The index theorem for quantum tori is linked to the quantum Hall effect,[4] and the index theorem for deformation quantization to the study of band energy redistribution in the Born-Oppenheimer approximation in molecular physics.[5]

See also

References

  1. ^ http://www.alainconnes.org/docs/SU(2)q.pdf
  2. ^ http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.47.1478
  3. ^ http://arxiv.org/abs/math/0408210v3
  4. ^ http://citeseer.ist.psu.edu/old/404503.html
  5. ^ http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.29.3618

External links