Bridge (graph theory)
In graph theory, a bridge (also known as a cut-edge or cut arc or an isthmus) is an edge whose deletion increases the number of connected components. Equivalently, an edge is a bridge if and only if it is not contained in any cycle.
A graph is said to be bridgeless if it contains no bridges. It is easy to see that this is equivalent to 2-edge-connectivity of each nontrivial component.
A graph with  nodes can contain at most
nodes can contain at most 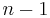 bridges, since adding additional edges must create a cycle.
bridges, since adding additional edges must create a cycle.
Contents |
Cycle double cover conjecture
An important open problem involving bridges is the cycle double cover conjecture, due to Seymour and Szekeres (1978 and 1979, independently), which states that every bridgeless graph admits a set of cycles which contains each edge exactly twice.[1]
Bridge-Finding Algorithm
An 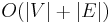 algorithm for finding bridges in a connected graph was found by Tarjan in 1974.[2] A distributed version of the algorithm also exists.[3]
algorithm for finding bridges in a connected graph was found by Tarjan in 1974.[2] A distributed version of the algorithm also exists.[3]
Algorithm:
- Find a spanning tree of

- Create a rooted tree
 from the spanning tree
from the spanning tree - Traverse the tree
 in preorder and number the nodes. Parent nodes in the tree now have lower numbers than child nodes.
in preorder and number the nodes. Parent nodes in the tree now have lower numbers than child nodes. - For each node from
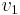 (the leaf nodes of the tree) to 1 (the root node of the tree) do:
(the leaf nodes of the tree) to 1 (the root node of the tree) do:
- Compute the number of descendants
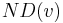 for this node.
for this node. - Compute
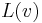 and
and 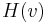
- For each
 such that
such that 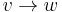 : if
: if 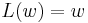 and
and 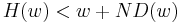 then
then 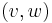 is a bridge.
is a bridge.
- Compute the number of descendants
Definitions: A non-tree (undirected) edge between  and
and  is denoted by
is denoted by 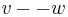 . An in-tree edge with
. An in-tree edge with  as the parent is denoted by
as the parent is denoted by 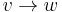 .
.
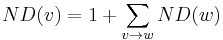 where
where  is the parent node of
is the parent node of  .
.
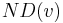 is the number of descendants of v (including itself) in the rooted spanning tree.
is the number of descendants of v (including itself) in the rooted spanning tree.
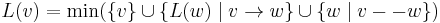
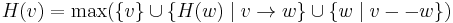
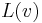 and
and 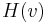 are the labels of the nodes with lowest and highest preorder label respectively reachable from v by travelling in the subtree rooted at v, along with at most one non-tree edge.
are the labels of the nodes with lowest and highest preorder label respectively reachable from v by travelling in the subtree rooted at v, along with at most one non-tree edge.
This algorithm works because 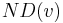 ,
, 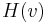 and
and 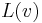 can all be computed for a node v provided we know their values on all in-tree descendants of v. Also, if and only if the edge
can all be computed for a node v provided we know their values on all in-tree descendants of v. Also, if and only if the edge 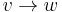 is a bridge, then it is clear that in the subtree rooted at
is a bridge, then it is clear that in the subtree rooted at  , it must be impossible to reach any node that is not a descendant of w. This is easy to check because the subtree rooted at w (that is, all descendants of w) consists of the nodes
, it must be impossible to reach any node that is not a descendant of w. This is easy to check because the subtree rooted at w (that is, all descendants of w) consists of the nodes 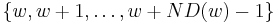 so we can simply check if
so we can simply check if 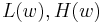 are in this set or not to check whether an edge is a bridge.
are in this set or not to check whether an edge is a bridge.
Cut arc in trees
An edge or arc e = uv of a tree G is a cut arc of G if and only if the degree of the vertices u and v are greater than 1. Cut arcs are also defined for directed graphs [4]
See also
Notes
- ^ http://www.cems.uvm.edu/%7Earchdeac/problems/cyclecov.htm
- ^ "A note on finding the bridges of a graph", Robert Endre Tarjan, Information Processing Letters, April 1974 pp160-161.
- ^ http://sma.epfl.ch/~pritchar/math/2006/podc-bicon-a0-poster.pdf
- ^ Rao, S.B.; Ramachandra Rao, A. The number of cut vertices and cut arcs in a strong directed graph. (English) Acta Math. Acad. Sci. Hung. 22, 411-421 (1972).
References
- Béla Bollobás, Modern graph theory, GTM 184, Springer Verlag, 1998. Page 6.
- Tarjan, Robert Endre. "A note on finding the bridges of a graph". Information Processing Letters 2 (6): 160–161. doi:10.1016/0020-0190(74)90003-9.