Cyclic redundancy check
A cyclic redundancy check (CRC) is an error-detecting code commonly used in digital networks and storage devices to detect accidental changes to raw data. Blocks of data entering these systems get a short check value attached, based on the remainder of a polynomial division of their contents; on retrieval the calculation is repeated, and corrective action can be taken against presumed data corruption if the check values do not match.
CRCs are so called because the check (data verification) value is a redundancy (it adds no information to the message) and the algorithm is based on cyclic codes. CRCs are popular because they are simple to implement in binary hardware, easy to analyze mathematically, and particularly good at detecting common errors caused by noise in transmission channels. Because the check value has a fixed length, the function that generates it is occasionally used as a hash function. The CRC was invented by W. Wesley Peterson in 1961; the 32-bit polynomial used in the CRC function of Ethernet and many other standards is the work of several researchers and was published in 1975.
Contents |
Introduction
CRCs are based on the theory of cyclic error-correcting codes. The use of systematic cyclic codes, which encode messages by adding a fixed-length check value, for the purpose of error detection in communication networks was first proposed by W. Wesley Peterson in 1961.[1] Cyclic codes are not only simple to implement but have the benefit of being particularly well suited for the detection of burst errors, contiguous sequences of erroneous data symbols in messages. This is important because burst errors are common transmission errors in many communication channels, including magnetic and optical storage devices. Typically an n-bit CRC applied to a data block of arbitrary length, will detect any single error burst not longer than n bits and will detect a fraction 1−2−n of all longer error bursts.
Specification of a CRC code requires definition of a so-called generator polynomial. This polynomial resembles the divisor in a polynomial long division, which takes the message as the dividend and in which the quotient is discarded and the remainder becomes the result, with the important distinction that the polynomial coefficients are calculated according to the carry-less arithmetic of a finite field. The length of the remainder is always less than the length of the generator polynomial, which therefore determines how long the result can be.
In practice, all commonly used CRCs employ the finite field GF(2). This is the field of two elements, usually called 0 and 1, comfortably matching computer architecture. The rest of this article will discuss only these binary CRCs, but the principles are more general.
The simplest error-detection system, the parity bit, is in fact a trivial 1-bit CRC: it uses the generator polynomial x+1.
Application
A CRC-enabled device calculates a short, fixed-length binary sequence, known as the check value or improperly the CRC, for each block of data to be sent or stored and appends it to the data, forming a codeword. When a codeword is received or read, the device either compares its check value with one freshly calculated from the data block, or equivalently, performs a CRC on the whole codeword and compares the resulting check value with an expected residue constant. If the check values do not match, then the block contains a data error and the device may take corrective action such as rereading or requesting the block be sent again, otherwise the data is assumed to be error-free (though, with some small probability, it may contain undetected errors; this is the fundamental nature of error-checking).[2]
CRCs and data integrity
CRCs are specifically designed to protect against common types of errors on communication channels, where they can provide quick and reasonable assurance of the integrity of messages delivered. However, they are not suitable for protecting against intentional alteration of data. Firstly, as there is no authentication, an attacker can edit a message and recalculate the CRC without the substitution being detected. This is even the case when the CRC is encrypted, leading to one of the design flaws of the WEP protocol.[3] Secondly, the linear properties of CRC codes even allow an attacker to modify a message in such a way as to leave the check value unchanged,[4][5] and otherwise permit efficient recalculation of the CRC for compact changes. Nonetheless, it is still often falsely assumed that when a message and its correct check value are received from an open channel then the message cannot have been altered in transit.[6]
Cryptographic hash functions, while still not providing security against intentional alteration when used in this manner, can provide stronger error checking in that they do not rely on specific error pattern assumptions. However, they are much slower than CRCs, and are therefore commonly used to protect off-line data, such as files on servers or databases.
When stored alongside the data, CRCs and cryptographic hash functions by themselves do not protect against intentional modification of data. Any application that requires protection against such attacks must use cryptographic authentication mechanisms, such as message authentication codes.
Computation of CRC
To compute an n-bit binary CRC, line the bits representing the input in a row, and position the (n+1)-bit pattern representing the CRC's divisor (called a "polynomial") underneath the left-hand end of the row.
Start with the message to be encoded:
11010011101100
This is first padded with zeroes corresponding to the bit length n of the CRC. Here is the first calculation for computing a 3-bit CRC:
11010011101100 000 <--- input left shifted by 3 bits 1011 <--- divisor (4 bits) = x³+x+1 ------------------ 01100011101100 000 <--- result
If the input bit above the leftmost divisor bit is 0, do nothing. If the input bit above the leftmost divisor bit is 1, the divisor is XORed into the input (in other words, the input bit above each 1-bit in the divisor is toggled). The divisor is then shifted one bit to the right, and the process is repeated until the divisor reaches the right-hand end of the input row. Here is the entire calculation:
11010011101100 000 <--- input left shifted by 3 bits
1011 <--- divisor
01100011101100 000 <--- result
1011 <--- divisor ...
00111011101100 000
1011
00010111101100 000
1011
00000001101100 000
1011
00000000110100 000
1011
00000000011000 000
1011
00000000001110 000
1011
00000000000101 000
101 1
-----------------
00000000000000 100 <---remainder (3 bits)
Since the leftmost divisor bit zeroed every input bit it touched, when this process ends the only bits in the input row that can be nonzero are the n bits at the right-hand end of the row. These n bits are the remainder of the division step, and will also be the value of the CRC function (unless the chosen CRC specification calls for some postprocessing).
The validity of a received message can easily be verified by performing the above calculation again, this time with the check value added instead of zeroes. The remainder should equal zero if there are no detectable errors.
11010011101100 100 <--- input with check value
1011 <--- divisor
01100011101100 100 <--- result
1011 <--- divisor ...
00111011101100 100
......
00000000001110 100
1011
00000000000101 100
101 1
------------------
0 <--- remainder
Mathematics of CRC
Mathematical analysis of this division-like process reveals how to pick a divisor that guarantees good error-detection properties. In this analysis, the digits of the bit strings are thought of as the coefficients of a polynomial in some variable x—coefficients that are elements of the finite field GF(2) instead of more familiar numbers. This binary polynomial is treated as a ring. A ring is, loosely speaking, a set of elements somewhat like numbers, that can be operated on by an operation that somewhat resembles addition and another operation that somewhat resembles multiplication, these operations possessing many of the familiar arithmetic properties of commutativity, associativity, and distributivity. Ring theory is part of abstract algebra.
Designing CRC polynomials
The selection of generator polynomial is the most important part of implementing the CRC algorithm. The polynomial must be chosen to maximize the error detecting capabilities while minimizing overall collision probabilities.
The most important attribute of the polynomial is its length (largest degree(exponent) +1 of any one term in the polynomial), because of its direct influence on the length of the computed check value.
The most commonly used polynomial lengths are:
- 9 bits (CRC-8)
- 17 bits (CRC-16)
- 33 bits (CRC-32)
- 65 bits (CRC-64)
The design of the CRC polynomial depends on the maximum total length of the block to be protected (data + CRC bits), the desired error protection features, and the type of resources for implementing the CRC as well as the desired performance. A common misconception is that the "best" CRC polynomials are derived from either an irreducible polynomial or an irreducible polynomial times the factor 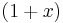 , which adds to the code the ability to detect all errors affecting an odd number of bits.[7] In reality, all the factors described above should enter in the selection of the polynomial. However, choosing a non-irreducible polynomial can result in missed errors due to the ring having zero divisors.
, which adds to the code the ability to detect all errors affecting an odd number of bits.[7] In reality, all the factors described above should enter in the selection of the polynomial. However, choosing a non-irreducible polynomial can result in missed errors due to the ring having zero divisors.
The advantage of choosing a primitive polynomial as the generator for a CRC code is that the resulting code has maximal total block length; in here if r is the degree of the primitive generator polynomial then the maximal total blocklength is equal to 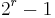 , and the associated code is able to detect any single bit or double errors.[8] If instead, we used as generator polynomial
, and the associated code is able to detect any single bit or double errors.[8] If instead, we used as generator polynomial 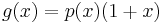 , where
, where 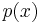 is a primitive polynomial of degree
is a primitive polynomial of degree 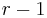 , then the maximal total blocklength would be equal to
, then the maximal total blocklength would be equal to 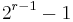 but the code would be able to detect single, double, and triple errors.
but the code would be able to detect single, double, and triple errors.
A polynomial 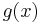 that admits other factorizations may be chosen then so as to balance the maximal total blocklength with a desired error detection power. A powerful class of such polynomials, which subsumes the two examples described above, is that of BCH codes. Regardless of the reducibility properties of a generator polynomial of degree r, assuming that it includes the "+1" term, such error detection code will be able to detect all error patterns that are confined to a window of r contiguous bits. These patterns are called "error bursts".
that admits other factorizations may be chosen then so as to balance the maximal total blocklength with a desired error detection power. A powerful class of such polynomials, which subsumes the two examples described above, is that of BCH codes. Regardless of the reducibility properties of a generator polynomial of degree r, assuming that it includes the "+1" term, such error detection code will be able to detect all error patterns that are confined to a window of r contiguous bits. These patterns are called "error bursts".
Specification of CRC
The concept of the CRC as an error-detecting code gets complicated when an implementer or standards committee turns it into a practical system. Here are some of the complications:
- Sometimes an implementation prefixes a fixed bit pattern to the bitstream to be checked. This is useful when clocking errors might insert 0-bits in front of a message, an alteration that would otherwise leave the check value unchanged.
- Sometimes an implementation appends n 0-bits (n being the size of the CRC) to the bitstream to be checked before the polynomial division occurs. This has the convenience that the remainder of the original bitstream with the check value appended is exactly zero, so the CRC can be checked simply by performing the polynomial division on the received bitstream and comparing the remainder with zero.
- Sometimes an implementation exclusive-ORs a fixed bit pattern into the remainder of the polynomial division.
- Bit order: Some schemes view the low-order bit of each byte as "first", which then during polynomial division means "leftmost", which is contrary to our customary understanding of "low-order". This convention makes sense when serial-port transmissions are CRC-checked in hardware, because some widespread serial-port transmission conventions transmit bytes least-significant bit first.
- Byte order: With multi-byte CRCs, there can be confusion over whether the byte transmitted first (or stored in the lowest-addressed byte of memory) is the least-significant byte or the most-significant byte. For example, some 16-bit CRC schemes swap the bytes of the check value.
- Omission of the high-order bit of the divisor polynomial: Since the high-order bit is always 1, and since an n-bit CRC must be defined by an (n+1)-bit divisor which overflows an n-bit register, some writers assume that it is unnecessary to mention the divisor's high-order bit.
- Omission of the low-order bit of the divisor polynomial: Since the low-order bit is always 1, authors such as Philip Koopman represent polynomials with their high-order bit intact, but without the low-order bit (the
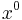 or 1 term). This convention encodes the polynomial complete with its degree in one integer.
or 1 term). This convention encodes the polynomial complete with its degree in one integer.
These complications mean that there are three common ways to express a polynomial as an integer: the first two, which are mirror images in binary, are the constants found in code; the third is the number found in Koopman's papers. In each case, one term is omitted. So the polynomial 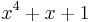 may be transcribed as:
may be transcribed as:
- 0x3 = 0011b, representing
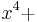
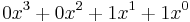 (MSB-first code)
(MSB-first code) - 0xC = 1100b, representing
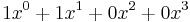
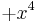
- 0x9 = 1001b, representing
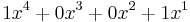
In the table below they are shown as:
| Representations: normal / reversed / reverse of reciprocal |
|---|
| 0x3 / 0xC / 0x9 |
Commonly used and standardized CRCs
Numerous varieties of cyclic redundancy check have been incorporated into technical standards. By no means does one algorithm, or one of each degree, suit every purpose; Koopman and Chakrabarty recommend selecting a polynomial according to the application requirements and the expected distribution of message lengths.[9] The number of distinct CRCs in use have however led to confusion among developers which authors have sought to address.[7] There are three polynomials reported for CRC-12,[9] sixteen conflicting definitions of CRC-16, and six of CRC-32.[10]
The polynomials commonly applied are not the most efficient ones possible. Between 1993 and 2004, Koopman, Castagnoli and others surveyed the space of polynomials up to 16 bits,[9] and of 24 and 32 bits,[11][12] finding examples that have much better performance (in terms of Hamming distance for a given message size) than the polynomials of earlier protocols, and publishing the best of these with the aim of improving the error detection capacity of future standards.[12] In particular, iSCSI and SCTP have adopted one of the findings of this research, the CRC-32C (Castagnoli) polynomial.
The design of the 32-bit polynomial most commonly used by standards bodies, CRC-32-IEEE, was the result of a joint effort for the Rome Laboratory and the Air Force Electronic Systems Division by Joseph Hammond, James Brown and Shyan-Shiang Liu of the Georgia Institute of Technology and Kenneth Brayer of the MITRE Corporation. The earliest known appearances of the 32-bit polynomial were in their 1975 publications: Technical Report 2956 by Brayer for MITRE, published in January and released for public dissemination through DTIC in August,[13] and Hammond, Brown and Liu's report for the Rome Laboratory, published in May.[14] Both reports contained contributions from the other team. In December 1975, Brayer and Hammond presented their work in a paper at the IEEE National Telecommunications Conference: the IEEE CRC-32 polynomial is the generating polynomial of a Hamming code and was selected for its error detection performance.[15] Even so, the Castagnoli CRC-32C polynomial used in iSCSI or SCTP matches its performance on messages from 58 bits–131 kbits, and outperforms it in several size ranges including the two most common sizes of Internet packet.[12] The ITU-T G.hn standard also uses CRC-32C to detect errors in the payload (although it uses CRC-16-CCITT for PHY headers).
The table below lists only the polynomials of the various algorithms in use. Variations of a particular protocol can impose pre-inversion, post-inversion and reversed bit ordering as described above. For example, the CRC32 used in both Gzip and Bzip2 use the same polynomial, but Bzip2 employs reversed bit ordering, while Gzip does not.
CRCs in proprietary protocols might use a non-trivial initial value and final XOR for obfuscation but this does not add cryptographic strength to the algorithm. An unknown error-detecting code can be characterized as a CRC, and as such fully reverse-engineered, from its output codewords.[16]
| Name | Polynomial | Representations: normal / reversed / reverse of reciprocal |
|---|---|---|
| CRC-1 | 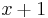 (most hardware; also known as parity bit) (most hardware; also known as parity bit) |
0x1 / 0x1 / 0x1 |
| CRC-4-ITU | 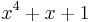 (ITU-T G.704, p. 12) (ITU-T G.704, p. 12) |
0x3 / 0xC / 0x9 |
| CRC-5-EPC | 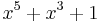 (Gen 2 RFID[17]) (Gen 2 RFID[17]) |
0x09 / 0x12 / 0x14 |
| CRC-5-ITU | 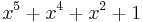 (ITU-T G.704, p. 9) (ITU-T G.704, p. 9) |
0x15 / 0x15 / 0x1A |
| CRC-5-USB | 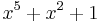 (USB token packets) (USB token packets) |
0x05 / 0x14 / 0x12 |
| CRC-6-ITU | 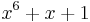 (ITU-T G.704, p. 3) (ITU-T G.704, p. 3) |
0x03 / 0x30 / 0x21 |
| CRC-7 | 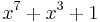 (telecom systems, ITU-T G.707, ITU-T G.832, MMC, SD) (telecom systems, ITU-T G.707, ITU-T G.832, MMC, SD) |
0x09 / 0x48 / 0x44 |
| CRC-8-CCITT | 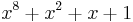 (ATM HEC), ISDN Header Error Control and Cell Delineation ITU-T I.432.1 (02/99) (ATM HEC), ISDN Header Error Control and Cell Delineation ITU-T I.432.1 (02/99) |
0x07 / 0xE0 / 0x83 |
| CRC-8-Dallas/Maxim | 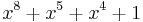 (1-Wire bus) (1-Wire bus) |
0x31 / 0x8C / 0x98 |
| CRC-8 | 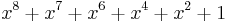 |
0xD5 / 0xAB / 0xEA[9] |
| CRC-8-SAE J1850 | 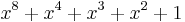 |
0x1D / 0xB8 / 0x8E |
| CRC-8-WCDMA | 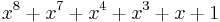 [18] [18] |
0x9B / 0xD9 / 0xCD[9] |
| CRC-10 | 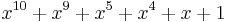 (ATM; ITU-T I.610) (ATM; ITU-T I.610) |
0x233 / 0x331 / 0x319 |
| CRC-11 | 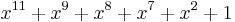 (FlexRay[19]) (FlexRay[19]) |
0x385 / 0x50E / 0x5C2 |
| CRC-12 | 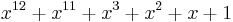 (telecom systems[20][21]) (telecom systems[20][21]) |
0x80F / 0xF01 / 0xC07[9] |
| CRC-15-CAN | 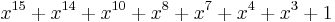 |
0x4599 / 0x4CD1 / 0x62CC |
| CRC-16-IBM | 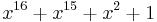 (Bisync, Modbus, USB, ANSI X3.28, many others; also known as CRC-16 and CRC-16-ANSI) (Bisync, Modbus, USB, ANSI X3.28, many others; also known as CRC-16 and CRC-16-ANSI) |
0x8005 / 0xA001 / 0xC002 |
| CRC-16-CCITT | 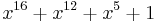 (X.25, V.41, HDLC, XMODEM, Bluetooth, SD, many others; known as CRC-CCITT) (X.25, V.41, HDLC, XMODEM, Bluetooth, SD, many others; known as CRC-CCITT) |
0x1021 / 0x8408 / 0x8810[9] |
| CRC-16-T10-DIF | 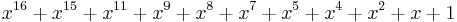 (SCSI DIF) (SCSI DIF) |
0x8BB7[22] / 0xEDD1 / 0xC5DB |
| CRC-16-DNP | 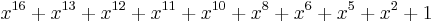 (DNP, IEC 870, M-Bus) (DNP, IEC 870, M-Bus) |
0x3D65 / 0xA6BC / 0x9EB2 |
| CRC-16-DECT | 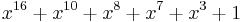 (cordless telephones)[23] (cordless telephones)[23] |
0x0589 / 0x91A0 / 0x82C4 |
| CRC-16-Fletcher | Not a CRC; see Fletcher's checksum | Used in Adler-32 A & B CRCs |
| CRC-24 | 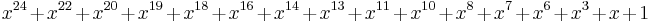 (FlexRay[19]) (FlexRay[19]) |
0x5D6DCB / 0xD3B6BA / 0xAEB6E5 |
| CRC-24-Radix-64 | 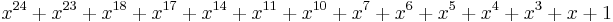 (OpenPGP) (OpenPGP) |
0x864CFB / 0xDF3261 / 0xC3267D |
| CRC-30 | 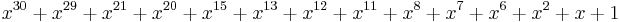 (CDMA) (CDMA) |
0x2030B9C7 / 0x38E74301 / 0x30185CE3 |
| CRC-32-Adler | Not a CRC; see Adler-32 | See Adler-32 |
| CRC-32 | 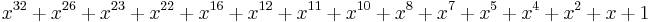 (ISO 3309, ANSI X3.66, FIPS PUB 71, FED-STD-1003, ITU-T V.42, Ethernet, SATA, MPEG-2, Gzip, PKZIP, POSIX cksum, PNG[24], ZMODEM) (ISO 3309, ANSI X3.66, FIPS PUB 71, FED-STD-1003, ITU-T V.42, Ethernet, SATA, MPEG-2, Gzip, PKZIP, POSIX cksum, PNG[24], ZMODEM) |
0x04C11DB7 / 0xEDB88320 / 0x82608EDB[12] |
| CRC-32C (Castagnoli) | 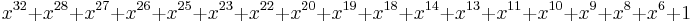 (iSCSI & SCTP, G.hn payload, SSE4.2) (iSCSI & SCTP, G.hn payload, SSE4.2) |
0x1EDC6F41 / 0x82F63B78 / 0x8F6E37A0[12] |
| CRC-32K (Koopman) | 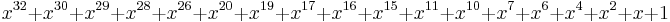 |
0x741B8CD7 / 0xEB31D82E / 0xBA0DC66B[12] |
| CRC-32Q | 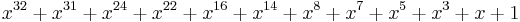 (aviation; AIXM[25]) (aviation; AIXM[25]) |
0x814141AB / 0xD5828281 / 0xC0A0A0D5 |
| CRC-40-GSM | 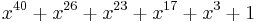 (GSM control channel[26][27]) (GSM control channel[26][27]) |
0x0004820009 / 0x9000412000 / 0x8002410004 |
| CRC-64-ISO | 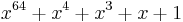 (HDLC — ISO 3309, Swiss-Prot/TrEMBL; considered weak for hashing[28]) (HDLC — ISO 3309, Swiss-Prot/TrEMBL; considered weak for hashing[28]) |
0x000000000000001B / 0xD800000000000000 / 0x800000000000000D |
| CRC-64-ECMA-182 | 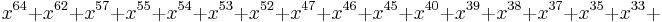 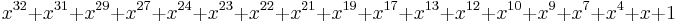 (as described in ECMA-182 p. 51) (as described in ECMA-182 p. 51) |
0x42F0E1EBA9EA3693 / 0xC96C5795D7870F42 / 0xA17870F5D4F51B49 |
See also
- Computation of CRC
- Error correcting code
- Cyclic code
- Redundancy check
- List of checksum algorithms
- Parity
- Information security
- Simple file verification
- cksum
- Header Error Correction
- Adler-32
- Fletcher's checksum
- Mathematics of CRCs
References
- ^ Peterson, W. W. and Brown, D. T. (January 1961). "Cyclic Codes for Error Detection". Proceedings of the IRE 49: 228. doi:10.1109/JRPROC.1961.287814.
- ^ Ritter, Terry (February 1986). "The Great CRC Mystery". Dr. Dobb's Journal 11 (2): 26–34, 76–83. http://www.ciphersbyritter.com/ARTS/CRCMYST.HTM. Retrieved 21 May 2009.
- ^ N. Cam-Winget, Nancy; R. Housley, Russ; D. Wagner, David; J. Walker, Jesse (May 2003). "Security Flaws in 802.11 Data Link Protocols". Communications of the ACM 46 (5): 35–39. doi:10.1145/769800.769823.
- ^ Stigge, Martin; Plötz, Henryk; Müller, Wolf; Redlich, Jens-Peter (May 2006). Reversing CRC – Theory and Practice. Berlin: Humboldt University Berlin. p. 17. http://sar.informatik.hu-berlin.de/research/publications/SAR-PR-2006-05/SAR-PR-2006-05_.pdf. Retrieved 4 February 2011. "The presented methods offer a very easy and efficient way to modify your data so that it will compute to a CRC you want or at least know in advance. This is not a very difficult task, as CRC is not a cryptographical hash algorithm [...] So you should never consider the CRC as some kind of message authentication code [...] – it can easily be forged."
- ^ Anachriz (30 April 1999). "CRC and how to Reverse it". http://www.woodmann.com/fravia/crctut1.htm. Retrieved 21 January 2010. Online essay with example x86 assembly code.
- ^ "Eurocontrol – FAQ: Technologies". European Organisation for the Safety of Air Navigation. http://www.eurocontrol.int/aim/public/faq/chain_faq3.html. Retrieved 29 April 2009. "A Cyclic Redundancy Check (CRC) is a means by which a data item may be assessed to verify that it has not been changed (either intentionally or unintentionally) since it the CRC value [sic] was applied to it."
- ^ a b Williams, Ross N. (24 September 1996). "A Painless Guide to CRC Error Detection Algorithms V3.00". http://www.repairfaq.org/filipg/LINK/F_crc_v3.html. Retrieved 5 June 2010.Contains a rigorous explanation of how to generate the CRC table typically found in implementations.
- ^ Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). "Section 22.4 Cyclic Redundancy and Other Checksums". Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8. http://apps.nrbook.com/empanel/index.html#pg=1168.
- ^ a b c d e f g Koopman, Philip; Chakravarty, Tridib (June 2004). "Cyclic Redundancy Code (CRC) Polynomial Selection For Embedded Networks". The International Conference on Dependable Systems and Networks: 145–154. doi:10.1109/DSN.2004.1311885. http://www.ece.cmu.edu/~koopman/roses/dsn04/koopman04_crc_poly_embedded.pdf. Retrieved 14 January 2011.
- ^ Cook, Greg (17 October 2011). "Catalogue of parametrised CRC algorithms". http://regregex.bbcmicro.net/crc-catalogue.htm. Retrieved 17 October 2011.
- ^ Castagnoli, G.; Bräuer, S.; Herrmann, M. (June 1993). "Optimization of Cyclic Redundancy-Check Codes with 24 and 32 Parity Bits". IEEE Transactions on Communications 41 (6): 883. doi:10.1109/26.231911. Castagnoli's et al. work on algorithmic selection of CRC polynomials.
- ^ a b c d e f Koopman, Philip (July 2002). "32-Bit Cyclic Redundancy Codes for Internet Applications". The International Conference on Dependable Systems and Networks: 459–468. doi:10.1109/DSN.2002.1028931. http://www.ece.cmu.edu/~koopman/networks/dsn02/dsn02_koopman.pdf. Retrieved 14 January 2011. Verification of Castagnoli's results by exhaustive search and some new good polynomials.
- ^ Brayer, Kenneth (August 1975). Evaluation of 32 Degree Polynomials in Error Detection on the SATIN IV Autovon Error Patterns. National Technical Information Service. p. 74. http://www.dtic.mil/srch/doc?collection=t3&id=ADA014825. Retrieved 3 February 2011.
- ^ Hammond, Joseph L., Jr.; Brown, James E.; Liu, Shyan-Shiang (May 1975). Development of a Transmission Error Model and an Error Control Model. National Technical Information Service. p. 74. Bibcode 1975STIN...7615344H. doi:100.2/ADA013939.
- ^ Brayer, Kenneth; Hammond, Joseph L., Jr. (December 1975). "Evaluation of error detection polynomial performance on the AUTOVON channel". Conference Record. 1. IEEE National Telecommunications Conference, New Orleans, La. New York: Institute of Electrical and Electronics Engineers. pp. 8–21 to 8–25. Bibcode 1975ntc.....1....8B.
- ^ Ewing, Gregory C. (March 2010). "Reverse-Engineering a CRC Algorithm". Christchurch: University of Canterbury. http://www.cosc.canterbury.ac.nz/greg.ewing/essays/CRC-Reverse-Engineering.html. Retrieved 26 July 2011.
- ^ Class-1 Generation-2 UHF RFID Protocol. 1.2.0. EPCglobal. 23 October 2008. p. 35. http://www.epcglobalinc.org/standards/uhfc1g2/uhfc1g2_1_0_9-standard-20050126.pdf. Retrieved 21 May 2009.
- ^ Richardson, Andrew (17 March 2005). WCDMA Handbook. Cambridge, UK: Cambridge University Press. p. 223. ISBN 0521828155.
- ^ a b FlexRay Protocol Specification. 2.1 Revision A. Flexray Consortium. 22 December 2005. p. 93.
- ^ Perez, A.; Wismer & Becker (1983). "Byte-Wise CRC Calculations". IEEE Micro 3 (3): 40–50. doi:10.1109/MM.1983.291120.
- ^ Ramabadran, T.V.; Gaitonde, S.S. (1988). "A tutorial on CRC computations". IEEE Micro 8 (4): 62–75. doi:10.1109/40.7773.
- ^ Thaler, Pat (28 August 2003). 16-bit CRC polynomial selection. INCITS T10. http://www.t10.org/ftp/t10/document.03/03-290r0.pdf. Retrieved 11 August 2009.
- ^ ETSI EN 300 175-3. V2.2.1. Sophia Antipolis, France: European Telecommunications Standards Institute. November 2008.
- ^ Boutell, Thomas; Randers-Pehrson, Glenn; et al. (14 July 1998). "PNG (Portable Network Graphics) Specification, Version 1.2". http://www.libpng.org/pub/png/spec/1.2/PNG-Structure.html. Retrieved 3 February 2011.
- ^ AIXM Primer. 4.5. European Organisation for the Safety of Air Navigation. 20 March 2006. http://www.eurocontrol.int/aim/gallery/content/public/aicm_aixm_4_5/aixm_primer/AIXM_Primer_4.5.pdf. Retrieved 29 April 2009.
- ^ Gammel, B.M. (31 October 2005). "Crypto - Codes". http://users.physik.tu-muenchen.de/gammel/matpack/html/LibDoc/Crypto/MpCRC.html. Retrieved 10 February 2011.
- ^ Geremia, Patrick (April 1999). Cyclic redundancy check computation: an implementation using the TMS320C54x. Texas Instruments. p. 5. http://focus.ti.com/lit/an/spra530/spra530.pdf. Retrieved 10 February 2011.
- ^ Jones, David T.. An Improved 64-bit Cyclic Redundancy Check for Protein Sequences. University College London. http://www.cs.ucl.ac.uk/staff/d.jones/crcnote.pdf. Retrieved 15 December 2009.
External links
- MathPages - Cyclic Redundancy Checks: overview with an explanation of error-detection of different polynomials.
- Clean C++ CRC32 Source Code; OS and Library Independent
- The CRC Pitstop - home of A Painless Guide to CRC Error Detection Algorithms
- Black, R. (1994-02) Fast CRC32 in Software; algorithm 4 is used in Linux and info-zip's zip and unzip.
- Kounavis, M. and Berry, F. (2005). A Systematic Approach to Building High Performance, Software-based, CRC generators, Slicing-by-4 and slicing-by-8 algorithms
- pycrc - a free C/C++ source code generator for various CRC algorithms
- CRC32: Generating a checksum for a file, C++ implementation by Brian Friesen
- The CRC++ Project Implementation in C++ which uses template classes to deal with different bit order
- 'CRC-Analysis with Bitfilters'.
- Cyclic Redundancy Check: theory, practice, hardware, and software with emphasis on CRC-32. A sample chapter from Henry S. Warren, Jr. Hacker's Delight.
- CRCs Code for CRC-32 and CRC-16 calculation in BASIC, 6502, Z80, PDP-11, 6809, 80x86, ARM and C.
- Reverse-Engineering a CRC Algorithm
|
||||||||