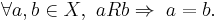Coreflexive relation

In mathematics, a coreflexive relation is a binary relation that is a subset of the identity relation.[1] Thus if a is related to b (aRb) then a is equal to b (a = b), but if c is equal to d (c = d) it does not necessarily hold that c is related to d (cRd).

In mathematical notation, this is:

\forall a, b \in X,\ a R b \Rightarrow \; a = b.

The identity relation is coreflexive by definition. Any relation that is coreflexive is thus a subset of the identity relation.

For example, consider the relation R as "equal to and odd". Over the set of positive integers, the relationship R holds over the pairs {(1, 1), (3, 3), ...} but does not hold over {(2, 2), (4, 4), ...}.

Notes

  1. ^ Fonseca de Oliveira, J. N., & Pereira Cunha Rodrigues, C. D. J. (2004). Transposing Relations: From Maybe Functions to Hash Tables. In Mathematics of Program Construction (p. 337).