Convex uniform honeycombs in hyperbolic space

In geometry, a convex uniform honeycomb is a tessellation of convex uniform polyhedron cells. In 3-dimensional hyperbolic space there are nine Coxeter group families of compact convex uniform honeycombs, generated as Wythoff constructions, and represented by ring permutations of the Coxeter–Dynkin diagrams for each family.

1 Nine Coxeter group families
- 1.1 Noncompact honeycombs
2 [3,5,3] family
3 [5,3,4] family
4 [5,3,5] family
5 [5,3^1,1] family
6 [(4,3,3,3)] family
7 [(5,3,3,3)] family
8 [(4,3,4,3)] family
9 [(4,3,5,3)] family
10 [(5,3,5,3)] family
11 See also
12 Notes
13 References

Nine Coxeter group families

By Coxeter group and Coxeter–Dynkin diagrams, the nine are:^[1]

#	Witt symbol	Coxeter symbol	Honeycombs
1	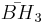${\bar{BH}}_3$	[4,3,5]	15 forms
2	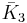${\bar{K}}_3$	[5,3,5]	9 forms
2	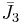${\bar{J}}_3$	[3,5,3]	9 forms
4	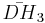${\bar{DH}}_3$	[5,3^1,1]	11 forms (7 overlap with [5,3,4] family, 4 are unique)
5	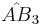${\hat{AB}}_3$	[(3,3,3,4)]	9 forms
6	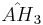${\hat{AH}}_3$	[(3,3,3,5)]	9 forms
7	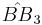${\hat{BB}}_3$	[(3,4,3,4)]	6 forms
8	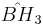${\hat{BH}}_3$	[(3,4,3,5)]	9 forms
9	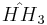${\hat{HH}}_3$	[(3,5,3,5)]	6 forms

These 9 families generate a total of 76 unique uniform honeycombs.

The full list of hyperbolic uniform honeycombs has not been proven and an unknown number of non-Wythoffian forms exist. One known example is cited with the {3,5,3} family below.

Noncompact honeycombs

There are also 23 noncompact Coxeter groups of rank 4. These families can produce uniform honeycombs with infinite or unbounded facets or vertex figure, including ideal vertices at infinity. These forms are not listed in this article.

Hyperbolic noncompact groups
Type	Coxeter groups	Group count	Honeycomb count
linear graphs	, , , , , ,	7	15+9+15+15+9+15+9=87
bifurcating graphs	, ,	3	11+11+7=29
cyclic graphs	, , , , , ,	7
mixed graphs	, , , , ,	6

[3,5,3] family

There are 9 forms, generated by ring permutations of the Coxeter group: [3,5,3] or

One related non-wythoffian form is constructed from the {3,5,3} vertex figure with 4 (tetrahedrally arranged) vertices removed, creating pentagonal antiprisms and dodecahedra filling in the gaps.^[2]

#	Honeycomb name Coxeter–Dynkin and Schläfli symbols	Cell counts/vertex and positions in honeycomb
#	Honeycomb name Coxeter–Dynkin and Schläfli symbols	0	1	2	3	Vertex figure	picture
1	icosahedral (Regular) t₀{3,5,3}				(20) (3.3.3.3.3)
2	rectified icosahedral t₁{3,5,3}	(2) (5.5.5)			(3) (3.5.3.5)
3	truncated icosahedral t_0,1{3,5,3}	(1) (5.5.5)			(3) (4.6.6)
4	cantellated icosahedral t_0,2{3,5,3}	(1) (3.5.3.5)	(2) (4.4.3)		(2) (3.5.4.5)
5	Runcinated icosahedral t_0,3{3,5,3}	(1) (3.3.3.3.3)	(5) (4.4.3)	(5) (4.4.3)	(1) (3.3.3.3.3)
6	bitruncated icosahedral t_1,2{3,5,3}	(2) (3.10.10)			(2) (3.10.10)
7	cantitruncated icosahedral t_0,1,2{3,5,3}	(1) (3.10.10)	(1) (4.4.3)		(2) (4.6.10)
8	runcitruncated icosahedral t_0,1,3{3,5,3}	(1) (3.5.4.5)	(1) (4.4.3)	(2) (4.4.6)	(1) (4.6.6)
9	omnitruncated icosahedral t_0,1,2,3{3,5,3}	(1) (4.6.10)	(1) (4.4.6)	(1) (4.4.6)	(1) (4.6.10)
[77]	partially truncated icosahedral pt{3,5,3}	(4) (5.5.5)			(12) (3.3.3.5)

[5,3,4] family

There are 15 forms, generated by ring permutations of the Coxeter group: [5,3,4] or

#	Name of honeycomb Coxeter–Dynkin diagram	Cells by location and count per vertex				Vertex figure	Picture
#	Name of honeycomb Coxeter–Dynkin diagram	0	1	2	3	Vertex figure	Picture
10	order-4 dodecahedral (Regular)	-	-	-	(8) (5.5.5)
11	Rectified order-4 dodecahedral	(2) (3.3.3.3)	-	-	(4) (3.5.3.5)
12	Rectified order-5 cubic	(5) (3.4.3.4)	-	-	(2) (3.3.3.3.3)
13	order-5 cubic (Regular)	(20) (4.4.4)	-	-	-
14	Truncated order-4 dodecahedral	(1) (3.3.3.3)	-	-	(4) (3.10.10)
15	Bitruncated order-5 cubic	(2) (4.6.6)	-	-	(2) (5.6.6)
16	Truncated order-5 cubic	(5) (3.8.8)	-	-	(1) (3.3.3.3.3)
17	Cantellated order-4 dodecahedral	(1) (3.4.3.4)	(2) (4.4.4)	-	(2) (3.4.5.4)
18	Cantellated order-5 cubic	(2) (3.4.4.4)	-	(2) (4.4.5)	(1) (3.5.3.5)
19	Runcinated order-5 cubic	(1) (4.4.4)	(3) (4.4.4)	(3) (4.4.5)	(1) (5.5.5)
20	Cantitruncated order-4 dodecahedral	(1) (4.6.6)	(1) (4.4.4)	-	(2) (4.6.10)
21	Cantitruncated order-5 cubic	(2) (4.6.8)	-	(1) (4.4.5)	(1) (5.6.6)
22	Runcitruncated order-4 dodecahedral	(1) (3.4.4.4)	(1) (4.4.4)	(2) (4.4.10)	(1) (3.10.10)
23	Runcitruncated order-5 cubic	(1) (3.8.8)	(2) (4.4.8)	(1) (4.4.5)	(1) (3.4.5.4)
24	Omnitruncated order-5 cubic	(1) (4.6.8)	(1) (4.4.8)	(1) (4.4.10)	(1) (4.6.10)
[34]	alternated order-5 cubic	(20) (3.3.3)			(12) (3.3.3.3)

[5,3,5] family

There are 9 forms, generated by ring permutations of the Coxeter group: [5,3,5] or

#	Name of honeycomb Coxeter–Dynkin diagram	Cells by location and count per vertex				Vertex figure
#	Name of honeycomb Coxeter–Dynkin diagram	0	1	2	3	Vertex figure
25	Order-5 dodecahedral t₀{5,3,5}				(20) (5.5.5)
26	rectified order-5 dodecahedral t₁{5,3,5}	(2) (3.3.3.3.3)			(5) (3.5.3.5)
27	truncated order-5 dodecahedral t_0,1{5,3,5}	(1) (3.3.3.3.3)			(5) (3.10.10)
28	cantellated order-5 dodecahedral t_0,2{5,3,5}	(1) (3.5.3.5)	(2) (4.4.5)		(2) (3.5.4.5)
29	Runcinated order-5 dodecahedral t_0,3{5,3,5}	(1) (5.5.5)	(3) (4.4.5)	(3) (4.4.5)	(1) (5.5.5)
30	bitruncated order-5 dodecahedral t_1,2{5,3,5}	(2) (4.6.6)			(2) (4.6.6)
31	cantitruncated order-5 dodecahedral t_0,1,2{5,3,5}	(1) (4.6.6)	(1) (4.4.5)		(2) (4.6.10)
32	runcitruncated order-5 dodecahedral t_0,1,3{5,3,5}	(1) (3.5.4.5)	(1) (4.4.5)	(2) (4.4.10)	(1) (3.10.10)
33	omnitruncated order-5 dodecahedral t_0,1,2,3{5,3,5}	(1) (4.6.10)	(1) (4.4.10)	(1) (4.4.10)	(1) (4.6.10)

[5,3^1,1] family

There are 11 forms (4 of which are not seen above), generated by ring permutations of the Coxeter group: [5,3^1,1] or

#	Honeycomb name Coxeter–Dynkin diagram	Cells by location (and count around each vertex)				vertex figure	Picture
#	Honeycomb name Coxeter–Dynkin diagram	0	1	0'	3	vertex figure	Picture
34	alternated order-5 cubic			(12) (3.3.3.3)	(20) (3.3.3)
35	truncated alternated order-5 cubic	(1) (3.5.3.5)		(2) (5.6.6)	(2) (3.6.6)
[11]	rectified order-4 dodecahedral (rectified alternated order-5 cubic)	(2) (3.5.3.5)		(2) (3.5.3.5)	(2) (3.3.3.3)
[12]	rectified order-5 cubic (cantellated alternated order-5 cubic)	(1) (3.3.3.3.3)		(1) (3.3.3.3.3)	(5) (3.4.3.4)
[15]	bitruncated order-5 cubic (cantitruncated alternated order-5 cubic)	(1) (5.6.6)		(1) (5.6.6)	(2) (4.6.6)
[14]	truncated order-4 dodecahedral (bicantellated alternated order-5 cubic)	(2) (3.10.10)		(2) (3.10.10)	(1) (3.3.3.3)
[10]	Order-4 dodecahedral (trirectified alternated order-5 cubic)	(4) (5.5.5)		(4) (5.5.5)
36	runcinated alternated order-5 cubic	(1) (3.3.3)		(3) (3.4.4.4)	(1) (3.3.3)
[17]	cantellated order-4 dodecahedral (runcicantellated alternated order-5 cubic)	(1) (3.4.5.4)	(2) (4.4.4)	(1) (3.4.5.4)	(1) (3.4.3.4)
37	runcitruncated alternated order-5 cubic	(1) (3.10.10)		(2) (4.6.10)	(1) (3.6.6)
[20]	cantitruncated order-4 dodecahedral (omnitruncated alternated order-5 cubic)	(1) (4.6.10)	(1) (4.4.4)	(1) (4.6.10)	(1) (4.6.6)

[(4,3,3,3)] family

There are 9 forms, generated by ring permutations of the Coxeter group:

#	Honeycomb name Coxeter–Dynkin diagram	Cells by location (and count around each vertex)				vertex figure
#	Honeycomb name Coxeter–Dynkin diagram	0	1	2	3	vertex figure
38		(4) (3.3.3)	-	(4) (4.4.4)	(6) (3.4.3.4)
39		(12) (3.3.3.3)	(8) (3.3.3)	-	(8) (3.3.3.3)
40		(3) (3.6.6)	(1) (3.3.3)	(1) (4.4.4)	(3) (4.6.6)
41		(1) (3.3.3)	(1) (3.3.3)	(3) (3.8.8)	(3) (3.8.8)
42		(4) (3.6.6)	(4) (3.6.6)	(1) (3.3.3.3)	(1) (3.3.3.3)
43		(1) (3.3.3.3)	(2) (3.4.3.4)	(1) (3.4.3.4)	(2) (3.4.4.4)
44		(1) (3.6.6)	(1) (3.4.3.4)	(1) (3.8.8)	(2) (4.6.8)
45		(2) (4.6.6)	(1) (3.6.6)	(1) (3.4.4.4)	(1) (4.6.6)
46		(1) (4.6.6)	(1) (4.6.6)	(1) (4.6.8)	(1) (4.6.8)

[(5,3,3,3)] family

There are 9 forms, generated by ring permutations of the Coxeter group:

#	Honeycomb name Coxeter–Dynkin diagram	Cells by location (and count around each vertex)				vertex figure
#	Honeycomb name Coxeter–Dynkin diagram	0	1	2	3	vertex figure
47		(4) (3.3.3)	-	(4) (5.5.5)	(6) (3.5.3.5)
48		(30) (3.3.3.3)	(20) (3.3.3)	-	(12) (3.3.3.3.3)
49		(3) (3.6.6)	(1) (3.3.3)	(1) (5.5.5)	(3) (5.6.6)
50		(1) (3.3.3)	(1) (3.3.3)	(3) (3.10.10)	(3) (3.10.10)
51		(5) (3.6.6)	(5) (3.6.6)	(1) (3.3.3.3.3)	(1) (3.3.3.3.3)
52		(1) (3.3.3.3)	(2) (3.4.3.4)	(1) (3.5.3.5)	(2) (3.4.5.4)
53		(1) (3.6.6)	(1) (3.4.3.4)	(1) (3.10.10)	(2) (4.6.10)
54		(2) (4.6.6)	(1) (3.6.6)	(1) (3.4.5.4)	(1) (5.6.6)
55		(1) (4.6.6)	(1) (4.6.6)	(1) (4.6.10)	(1) (4.6.10)

[(4,3,4,3)] family

There are 6 forms, generated by ring permutations of the Coxeter group:

#	Honeycomb name Coxeter–Dynkin diagram	Cells by location (and count around each vertex)				vertex figure
#	Honeycomb name Coxeter–Dynkin diagram	0	1	2	3	vertex figure
56		(6) (3.3.3.3)	-	(8) (4.4.4)	(12) (3.4.3.4)
57		(3) (4.6.6)	(1) (4.4.4)	(1) (4.4.4)	(3) (4.6.6)
58		(1) (3.3.3.3)	(1) (3.3.3.3)	(3) (3.8.8)	(3) (3.8.8)
59		(1) (3.4.3.4)	(2) (3.4.4.4)	(1) (3.4.3.4)	(2) (3.4.4.4)
60		(1) (4.6.6)	(1) (3.4.4.4)	(1) (3.8.8)	(2) (4.6.8)
61		(1) (4.6.8)	(1) (4.6.8)	(1) (4.6.8)	(1) (4.6.8)

[(4,3,5,3)] family

There are 9 forms, generated by ring permutations of the Coxeter group:

#	Honeycomb name Coxeter–Dynkin diagram	Cells by location (and count around each vertex)				vertex figure
#	Honeycomb name Coxeter–Dynkin diagram	0	1	2	3	vertex figure
62		(6) (3.3.3.3)	-	(8) (5.5.5)	(1) (3.5.3.5)
63		(30) (3.4.3.4)	(20) (4.4.4)	-	(12) (3.3.3.3.3)
64		(3) (4.6.6)	(1) (4.4.4)	(1) (5.5.5)	(3) (5.6.6)
65		(1) (3.3.3.3)	(1) (3.3.3.3)	(4) (3.10.10)	(4) (3.10.10)
66		(5) (3.8.8)	(5) (3.8.8)	(1) (3.3.3.3.3)	(1) (3.3.3.3.3)
67		(1) (3.4.3.4)	(2) (3.4.4.4)	(1) (3.5.3.5)	(2) (3.4.5.4)
68		(1) (4.6.6)	(1) (3.4.4.4)	(1) (3.10.10)	(2) (4.6.10)
69		(2) (4.6.8)	(1) (3.8.8)	(1) (3.4.5.4)	(1) (5.6.6)
70		(1) (4.6.8)	(1) (4.6.8)	(1) (4.6.10)	(1) (4.6.10)

[(5,3,5,3)] family

There are 6 forms, generated by ring permutations of the Coxeter group:

#	Honeycomb name Coxeter–Dynkin diagram	Cells by location (and count around each vertex)				vertex figure
#	Honeycomb name Coxeter–Dynkin diagram	0	1	2	3	vertex figure
71		(12) (3.3.3.3.3)	-	(20) (5.5.5)	(30) (3.5.3.5)
72		(3) (5.6.6)	(1) (5.5.5)	(1) (5.5.5)	(3) (5.6.6)
73		(1) (3.3.3.3.3)	(1) (3.3.3.3.3)	(3) (3.10.10)	(3) (3.10.10)
74		(1) (3.5.3.5)	(2) (3.4.5.4)	(1) (3.5.3.5)	(2) (3.4.5.4)
75		(1) (5.6.6)	(1) (3.4.5.4)	(1) (3.10.10)	(2) (4.6.10)
76		(1) (4.6.10)	(1) (4.6.10)	(1) (4.6.10)	(1) (4.6.10)

Notes

^ Humphreys, 1990, page 141, 6.9 List of hyperbolic Coxeter groups, figure 2 [1]
^ Wendy Y. Krieger, Walls and bridges: The view from six dimensions, Symmetry: Culture and Science Volume 16, Number 2, pages 171-192 (2005) [2]

References

James E. Humphreys, Reflection Groups and Coxeter Groups, Cambridge studies in advanced mathematics, 29 (1990)
The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678, ISBN 0-486-40919-8 (Chapter 10, Regular Honeycombs in Hyperbolic Space)
Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8. (Tables I and II: Regular polytopes and honeycombs, pp. 294-296)
Jeffrey R. Weeks The Shape of Space, 2nd edition ISBN 0-8247-0709-5 (Chapter 16-17: Geometries on Three-manifolds I,II) [3]

Convex uniform honeycombs in hyperbolic space

Contents

Nine Coxeter group families

Noncompact honeycombs

[3,5,3] family

[5,3,4] family

[5,3,5] family

[5,31,1] family

[(4,3,3,3)] family

[(5,3,3,3)] family

[(4,3,4,3)] family

[(4,3,5,3)] family

[(5,3,5,3)] family

See also

Notes

References

[5,3^1,1] family