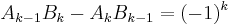Convergent (continued fraction)

A convergent is one of a sequence of values obtained by evaluating successive truncations of a continued fraction.[1][2] The nth convergent is also known as the nth approximant of a continued fraction.[3]

Contents

Representation of real numbers

Every real number can be expressed as a regular continued fraction in canonical form. Each convergent of that continued fraction is in a sense the best possible rational approximation to that real number, for a given number of digits. Such a convergent is usually about as accurate as a finite decimal expansion having as many digits as the total number of digits in the nth numerator and nth denominator. For example, the third convergent 333/106 for π (Pi) is roughly 3.1415094, which is not quite as accurate as the 6-digit 3.14159; the fourth convergent 355/113 = 3.14159292 is more accurate than the 6-digit decimal.

By the determinant formula it appears that the successive convergents Ak/Bk of a regular continued fraction are connected by the formula

A_{k-1}B_k - A_kB_{k-1} = (-1)^k \,

This implies, in particular, that the greatest common divisor (Ak, Bk) = 1; in other words, each convergent of a regular continued fraction, as given by the fundamental recurrence formulas, is automatically expressed in lowest terms.

More detailed properties of best rational approximations and convergents of π are discussed in the continued fraction article.

Convergents and convergence

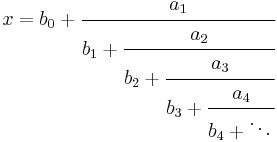
In mathematical analysis a continued fraction is usually written as

x = b_0 %2B \cfrac{a_1}{b_1 %2B \cfrac{a_2}{b_2 %2B \cfrac{a_3}{b_3 %2B \cfrac{a_4} {b_4 %2B \ddots\,}}}}

where the ai and the bi are integers. The ai are the partial numerators of the continued fraction x. The bi are the partial denominators, and the ratios ai / bi are the partial quotients. The convergents of this fraction can be computed by using the fundamental recurrence formulas.

An infinite continued fraction converges if the sequence of convergents approaches a limit. If the sequence of convergents does not approach a limit, the continued fraction is divergent.

Because of the way the partial denominators and partial numerators interact with each other as the successive convergents are calculated, the convergence problem for continued fractions is inherently more difficult than it is for infinite series. The Śleszyński–Pringsheim theorem provides one sufficient condition for convergence.

See also

Notes

  1. ^ Long (1972, p. 177)
  2. ^ Pettofrezzo & Byrkit (1970, p. 162)
  3. ^ Nechaev, V.I. (2001), "Continued fraction", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=C/c025540 

References