Convergence tests
In mathematics, convergence tests are methods of testing for the convergence, conditional convergence, absolute convergence, interval of convergence or divergence of an infinite series.
Contents |
List of tests
- Limit of the summand. If the limit of the summand is undefined or nonzero, that is
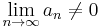 , then the series must diverge. In this sense, the partial sums are Cauchy only if this limit exists and is equal to zero. The test is inconclusive if the limit of the summand is zero.
, then the series must diverge. In this sense, the partial sums are Cauchy only if this limit exists and is equal to zero. The test is inconclusive if the limit of the summand is zero.
- Ratio test (D'Alembert's criterion). Suppose that there exists
 such that
such that
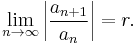
- If r < 1, then the series converges. If r > 1, then the series diverges. If r = 1, the ratio test is inconclusive, and the series may converge or diverge.
- Root test or nth root test (Cauchy's criterion). Define r as follows:
- where "lim sup" denotes the limit superior (possibly ∞; if the limit exists it is the same value).
- If r < 1, then the series converges. If r > 1, then the series diverges. If r = 1, the root test is inconclusive, and the series may converge or diverge.
- Integral test. The series can be compared to an integral to establish convergence or divergence. Let
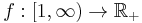 be a positive and monotone decreasing function such that
be a positive and monotone decreasing function such that 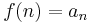 . If
. If
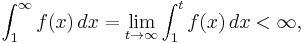
- then the series converges. But if the integral diverges, then the series does so as well.
- In other words, the series
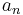 converges if and only if the integral converges.
converges if and only if the integral converges.
- Direct comparison test. If the series
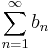 is an absolutely convergent series and
is an absolutely convergent series and 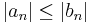 for sufficiently large n , then the series
for sufficiently large n , then the series 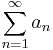 converges absolutely.
converges absolutely.
- Limit comparison test. If
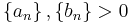 , and the limit
, and the limit 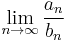 exists and is not zero, then
exists and is not zero, then 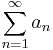 converges if and only if
converges if and only if 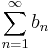 converges.
converges.
- Cauchy condensation test. Let
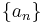 be a positive non-increasing sequence. Then the sum
be a positive non-increasing sequence. Then the sum 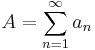 converges if and only if the sum
converges if and only if the sum 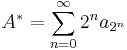 converges. Moreover, if they converge, then
converges. Moreover, if they converge, then 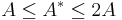 holds.
holds.
- Alternating series test (Leibniz criterion)
- For some specific types of series there are more specialized convergence tests, for instance for Fourier series there is the Dini test.
Comparison
The root test is stronger than the ratio test (it is more powerful because the required condition is weaker): whenever the ratio test determines the convergence or divergence of an infinite series, the root test does too, but not conversely.[1]
For example, for the series
- 1 + 1 + 0.5 + 0.5 + 0.25 + 0.25 + 0.125 + 0.125 + ...=4
convergence follows from the root test but not from the ratio test.
Examples
Consider the series
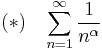 .
.
Cauchy condensation test implies that (*) is finitely convergent if
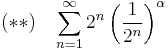
is finitely convergent. Since
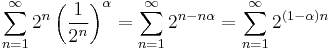
(**) is geometric series with ratio 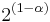 . (**) is finitely convergent if its ratio is less than one (namely
. (**) is finitely convergent if its ratio is less than one (namely 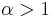 ). Thus, (*) is finitely convergent if and only if
). Thus, (*) is finitely convergent if and only if 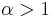 .
.
Convergence of products
While most of the tests deal with the convergence of infinite series, they can also be used to show the convergence or divergence of infinite products. This can be achieved using following theorem: Let 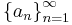 be a sequence of positive numbers. Then the infinite product
be a sequence of positive numbers. Then the infinite product 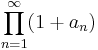 converges if and only if the series
converges if and only if the series 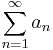 converges. Also similarly, if
converges. Also similarly, if 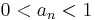 holds, then
holds, then 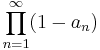 approaches a non-zero limit if and only if the series
approaches a non-zero limit if and only if the series 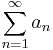 converges .
converges .
This can be proved by taking logarithm of the product and using limit comparison test.[2]
![r = \limsup_{n \to \infty}\sqrt[n]{|a_n|},](/2012-wikipedia_en_all_nopic_01_2012/I/234327a2c3bdded4b3fcb51ef3412c09.png)