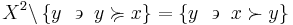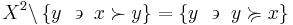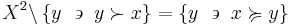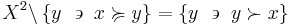Contour set
In mathematics, contour sets generalize and formalize the everyday notions of
- everything superior to something
- everything superior or equivalent to something
- everything inferior to something
- everything inferior or equivalent to something.
Contents |
Formal definitions
Given a relation on pairs of elements of set 
and an element  of
of 
The upper contour set of  is the set of all
is the set of all  that are related to
that are related to  :
:
The lower contour set of  is the set of all
is the set of all  such that
such that  is related to them:
is related to them:
The strict upper contour set of  is the set of all
is the set of all  that are related to
that are related to  without
without  being in this way related to any of them:
being in this way related to any of them:
The strict lower contour set of  is the set of all
is the set of all  such that
such that  is related to them without any of them being in this way related to
is related to them without any of them being in this way related to  :
:
The formal expressions of the last two may be simplified if we have defined
so that  is related to
is related to  but
but  is not related to
is not related to  , in which case the strict upper contour set of
, in which case the strict upper contour set of  is
is
and the strict lower contour set of  is
is
Contour sets of a function
In the case of a function 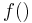 considered in terms of relation
considered in terms of relation 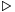 , reference to the contour sets of the function is implicitly to the contour sets of the implied relation
, reference to the contour sets of the function is implicitly to the contour sets of the implied relation
Examples
Arithmetic
Consider a real number  , and the relation
, and the relation 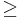 . Then
. Then
- the upper contour set of
 would be the set of numbers that were greater than or equal to
would be the set of numbers that were greater than or equal to  ,
, - the strict upper contour set of
 would be the set of numbers that were greater than
would be the set of numbers that were greater than  ,
, - the lower contour set of
 would be the set of numbers that were less than or equal to
would be the set of numbers that were less than or equal to  , and
, and - the strict lower contour set of
 would be the set of numbers that were less than
would be the set of numbers that were less than  .
.
Consider, more generally, the relation
Then
- the upper contour set of
 would be the set of all
would be the set of all  such that
such that  ,
, - the strict upper contour set of
 would be the set of all
would be the set of all  such that
such that 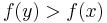 ,
, - the lower contour set of
 would be the set of all
would be the set of all  such that
such that 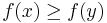 , and
, and - the strict lower contour set of
 would be the set of all
would be the set of all  such that
such that  .
.
It would be technically possible to define contour sets in terms of the relation
though such definitions would tend to confound ready understanding.
In the case of a real-valued function 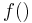 (whose arguments might or might not be themselves real numbers), reference to the contour sets of the function is implicitly to the contour sets of the relation
(whose arguments might or might not be themselves real numbers), reference to the contour sets of the function is implicitly to the contour sets of the relation
Note that the arguments to 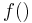 might be vectors, and that the notation used might instead be
might be vectors, and that the notation used might instead be
Economic
In economics, the set  could be interpreted as a set of goods and services or of possible outcomes, the relation
could be interpreted as a set of goods and services or of possible outcomes, the relation  as strict preference, and the relationship
as strict preference, and the relationship 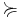 as weak preference. Then
as weak preference. Then
- the upper contour set of
 would be the set of all goods, services, or outcomes that were at least as desired as
would be the set of all goods, services, or outcomes that were at least as desired as  ,
, - the strict upper contour set of
 would be the set of all goods, services, or outcomes that were more desired than
would be the set of all goods, services, or outcomes that were more desired than  ,
, - the lower contour set of
 would be the set of all goods, services, or outcomes that were no more desired than
would be the set of all goods, services, or outcomes that were no more desired than  , and
, and - the strict lower contour set of
 would be the set of all goods, services, or outcomes that were less desired than
would be the set of all goods, services, or outcomes that were less desired than  .
.
Such preferences might be captured by a utility function 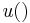 , in which case
, in which case
- the upper contour set of
 would be the set of all
would be the set of all  such that
such that 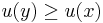 ,
, - the strict upper contour set of
 would be the set of all
would be the set of all  such that
such that  ,
, - the lower contour set of
 would be the set of all
would be the set of all  such that
such that 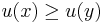 , and
, and - the strict lower contour set of
 would be the set of all
would be the set of all  such that
such that 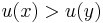 .
.
Complementarity
On the assumption that 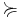 is a total ordering of
is a total ordering of  , the complement of the upper contour set is the strict lower contour set.
, the complement of the upper contour set is the strict lower contour set.
and the complement of the strict upper contour set is the lower contour set.
See also
References
- Andreu Mas-Colell, Michael D. Whinston, and Jerry R. Green; Microeconomic Theory (LCC HB172.M6247 1995), p43. ISBN 0-19-507340-1 (cloth) ISBN 0-19-510268-1 (paper)
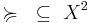
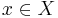
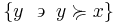
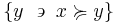


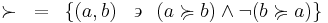
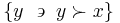
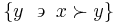
![(a\succcurlyeq b)~\Leftarrow~[f(a)\triangleright f(b)]](/2012-wikipedia_en_all_nopic_01_2012/I/ea6e102dc189a375cd3c84f5b5e434b2.png)
![(a\succcurlyeq b)~\Leftarrow~[f(a)\ge f(b)]](/2012-wikipedia_en_all_nopic_01_2012/I/59d7539e2775148fe3d8bb0fca2c70a6.png)
![(a\succcurlyeq b)~\Leftarrow~[f(a)\le f(b)]](/2012-wikipedia_en_all_nopic_01_2012/I/9a654da54f286ef40349ba7278141d10.png)
![[(a_1 ,a_2 ,\ldots)\succcurlyeq(b_1 ,b_2 ,\ldots)]~\Leftarrow~[f(a_1 ,a_2 ,\ldots)\ge f(b_1 ,b_2 ,\ldots)]](/2012-wikipedia_en_all_nopic_01_2012/I/0c669b3bf0b7a564662233f0fb16db21.png)