Context-free language
In formal language theory, a context-free language is a language generated by some context-free grammar. The set of all context-free languages is identical to the set of languages accepted by pushdown automata.
Contents |
Examples
An archetypical context-free language is 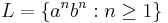 , the language of all non-empty even-length strings, the entire first halves of which are
, the language of all non-empty even-length strings, the entire first halves of which are  's, and the entire second halves of which are
's, and the entire second halves of which are  's.
's.  is generated by the grammar
is generated by the grammar 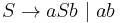 , and is accepted by the pushdown automaton
, and is accepted by the pushdown automaton 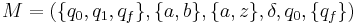 where
where  is defined as follows:
is defined as follows:
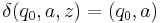
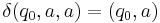
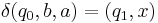
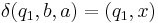
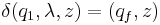
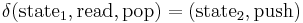
where 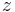 is initial stack symbol and
is initial stack symbol and  means pop action.
means pop action.
Context-free languages have many applications in programming languages; for example, the language of all properly matched parentheses is generated by the grammar 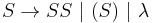 . Also, most arithmetic expressions are generated by context-free grammars.
. Also, most arithmetic expressions are generated by context-free grammars.
Closure properties
Context-free languages are closed under the following operations. That is, if L and P are context-free languages, the following languages are context-free as well:
- the union
 of L and P
of L and P - the reversal of L
- the concatenation
 of L and P
of L and P - the Kleene star
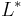 of L
of L - the image φ(L) of L under a homomorphism φ
- the image
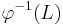 of L under an inverse homomorphism
of L under an inverse homomorphism 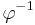
- the cyclic shift of L (the language
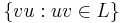 )
)
Context-free languages are not closed under complement, intersection, or difference. However, if L is a context-free language and D is a regular language then both their intersection  and their difference
and their difference 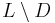 are context-free languages.
are context-free languages.
Nonclosure under intersection and complement
The context-free languages are not closed under intersection. This can be seen by taking the languages 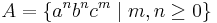 and
and 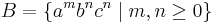 , which are both context-free. Their intersection is
, which are both context-free. Their intersection is 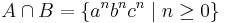 , which can be shown to be non-context-free by the pumping lemma for context-free languages.
, which can be shown to be non-context-free by the pumping lemma for context-free languages.
Context-free languages are also not closed under complementation, as for any languages A and B: 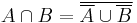 .
.
Decidability properties
The following problems are undecidable for arbitrary context-free grammars A and B:
- Equivalence: is
 ?
? - is
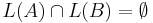 ? (However, the intersection of a context-free language and a regular language is context-free, so if
? (However, the intersection of a context-free language and a regular language is context-free, so if  were a regular language, this problem becomes decidable.)
were a regular language, this problem becomes decidable.) - is
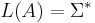 ?
? - is
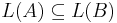 ?
?
The following problems are decidable for arbitrary context-free languages:
- is
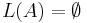 ?
? - is
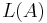 finite?
finite? - Membership: given any word
 , does
, does 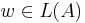 ? (membership problem is even polynomially decidable - see CYK algorithm and Early's Algorithm)
? (membership problem is even polynomially decidable - see CYK algorithm and Early's Algorithm)
Properties of context-free languages
- The reverse of a context-free language is context-free, but the complement need not be.
- Every regular language is context-free because it can be described by a context-free grammar.
- The intersection of a context-free language and a regular language is always context-free.
- There exist context-sensitive languages which are not context-free.
- To prove that a given language is not context-free, one may employ the pumping lemma for context-free languages.
References
- Seymour Ginsburg (1966). The Mathematical Theory of Context-Free Languages. New York, NY, USA: McGraw-Hill, Inc..
- Michael Sipser (1997). Introduction to the Theory of Computation. PWS Publishing. ISBN 0-534-94728-X. Chapter 2: Context-Free Languages, pp. 91–122.
- Jean-Michel Autebert, Jean Berstel, Luc Boasson, Context-Free Languages and Push-Down Automata, in: G. Rozenberg, A. Salomaa (eds.), Handbook of Formal Languages, Vol. 1, Springer-Verlag, 1997, 111-174.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||