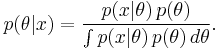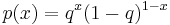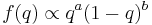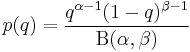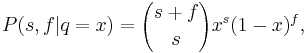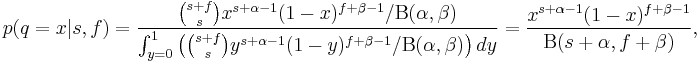Conjugate prior
In Bayesian probability theory, if the posterior distributions p(θ|x) are in the same family as the prior probability distribution p(θ), the prior and posterior are then called conjugate distributions, and the prior is called a conjugate prior for the likelihood. For example, the Gaussian family is conjugate to itself (or self-conjugate) with respect to a Gaussian likelihood function: if the likelihood function is Gaussian, choosing a Gaussian prior over the mean will ensure that the posterior distribution is also Gaussian. The concept, as well as the term "conjugate prior", were introduced by Howard Raiffa and Robert Schlaifer in their work on Bayesian decision theory.[1] A similar concept had been discovered independently by George Alfred Barnard.[2]
Consider the general problem of inferring a distribution for a parameter θ given some datum or data x. From Bayes' theorem, the posterior distribution is equal to the product of the likelihood function 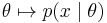 and prior p(θ), normalized (divided) by the probability of the data p(x):
and prior p(θ), normalized (divided) by the probability of the data p(x):
Let the likelihood function be considered fixed; the likelihood function is usually well-determined from a statement of the data-generating process. It is clear that different choices of the prior distribution p(θ) may make the integral more or less difficult to calculate, and the product p(x|θ) × p(θ) may take one algebraic form or another. For certain choices of the prior, the posterior has the same algebraic form as the prior (generally with different parameter values). Such a choice is a conjugate prior.
A conjugate prior is an algebraic convenience, giving a closed-form expression for the posterior: otherwise a difficult numerical integration may be necessary. Further, conjugate priors may give intuition, by more transparently showing how a likelihood function updates a distribution.
All members of the exponential family have conjugate priors. See Gelman et al.[3] for a catalog.
Contents |
Example
The form of the conjugate prior can generally be determined by inspection of the probability density or probability mass function of a distribution. For example, consider a random variable which is a Bernoulli trial with unknown probability of success q in [0,1]. The probability density function has the form
Expressed as a function of  , this has the form
, this has the form
for some constants  and
and  . Generally, this functional form will have an additional multiplicative factor (the normalizing constant) ensuring that the function is a probability distribution, i.e. the integral over the entire range is 1. This factor will often be a function of
. Generally, this functional form will have an additional multiplicative factor (the normalizing constant) ensuring that the function is a probability distribution, i.e. the integral over the entire range is 1. This factor will often be a function of  and
and  , but never of
, but never of  .
.
In fact, the usual conjugate prior is the beta distribution with
where  and
and  are chosen to reflect any existing belief or information (
are chosen to reflect any existing belief or information ( = 1 and
= 1 and  = 1 would give a uniform distribution) and Β(
= 1 would give a uniform distribution) and Β( ,
,  ) is the Beta function acting as a normalising constant.
) is the Beta function acting as a normalising constant.
In this context,  and
and  are called hyperparameters (parameters of the prior), to distinguish them from parameters of the underlying model (here q). It is a typical characteristic of conjugate priors that the dimensionality of the hyperparameters is one greater than that of the parameters of the original distribution. If all parameters are scalar values, then this means that there will be one more hyperparameter than parameter; but this also applies to vector-valued and matrix-valued parameters. (See the general article on the exponential family, and consider also the Wishart distribution, conjugate prior of the covariance matrix of a multivariate normal distribution, for an example where a large dimensionality is involved.)
are called hyperparameters (parameters of the prior), to distinguish them from parameters of the underlying model (here q). It is a typical characteristic of conjugate priors that the dimensionality of the hyperparameters is one greater than that of the parameters of the original distribution. If all parameters are scalar values, then this means that there will be one more hyperparameter than parameter; but this also applies to vector-valued and matrix-valued parameters. (See the general article on the exponential family, and consider also the Wishart distribution, conjugate prior of the covariance matrix of a multivariate normal distribution, for an example where a large dimensionality is involved.)
If we then sample this random variable and get s successes and f failures, we have
which is another Beta distribution with a simple change to the (hyper)parameters. This posterior distribution could then be used as the prior for more samples, with the hyperparameters simply adding each extra piece of information as it comes.
Interpretations
Analogy with eigenfunctions
Conjugate priors are analogous to eigenfunctions in operator theory, in that they are distributions on which the "conditioning operator" acts in a well-understood way, thinking of the process of changing from the prior to the posterior as an operator.
In both eigenfunctions and conjugate priors, there is a finite dimensional space which is preserved by the operator: the output is of the same form (in the same space) as the input. This greatly simplifies the analysis, as it otherwise considers an infinite dimensional space (space of all functions, space of all distributions).
However, the processes are only analogous, not identical: conditioning is not linear, as the space of distributions is not closed under linear combination, only convex combination, and the posterior is only of the same form as the prior, not a scalar multiple.
Just as one can easily analyze how a linear combination of eigenfunctions evolves under application of an operator (because, with respect to these functions, the operator is diagonalized), one can easily analyze how a convex combination of conjugate priors evolves under conditioning; this is called using a hyperprior, and corresponds to using a mixture density of conjugate priors, rather than a single conjugate prior.
Dynamical system
One can think of conditioning on conjugate priors as defining a kind of (discrete time) dynamical system: from a given set of hyperparameters, incoming data updates these hyperparameters, so one can see the change in hyperparameters as a kind of "time evolution" of the system, corresponding to "learning". Starting at different points yields different flows over time. This is again analogous with the dynamical system defined by a linear operator, but note that since different samples lead to different inference, this is not simply dependent on time, but rather on data over time. For related approaches, see Recursive Bayesian estimation and Data assimilation.
Table of conjugate distributions
Let n denote the number of observations.
If the likelihood function belongs to the exponential family, then a conjugate prior exists, often also in the exponential family; see Exponential family: Conjugate distributions.
Discrete likelihood distributions
| Likelihood | Model parameters | Conjugate prior distribution | Prior hyperparameters | Posterior hyperparameters |
|---|---|---|---|---|
| Bernoulli | p (probability) | Beta | 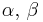 |
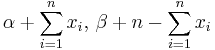 |
| Binomial | p (probability) | Beta | 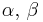 |
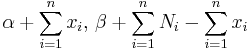 |
| Negative Binomial | p (probability) | Beta | 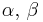 |
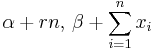 |
| Poisson | λ (rate) | Gamma | 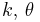 |
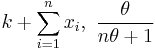 |
| Poisson | λ (rate) | Gamma | 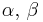 [4] [4] |
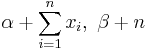 |
| Multinomial | p (probability vector) | Dirichlet | 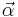 |
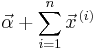 |
| Geometric | p0 (probability) | Beta | 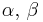 |
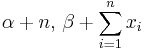 |
Continuous likelihood distributions
| Likelihood | Model parameters | Conjugate prior distribution | Prior hyperparameters | Posterior hyperparameters |
|---|---|---|---|---|
| Uniform | 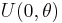 |
Pareto | 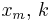 |
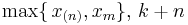 |
| Exponential | λ (rate) | Gamma | 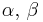 [4] [4] |
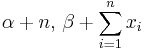 |
| Normal with known variance σ2 |
μ (mean) | Normal | 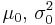 |
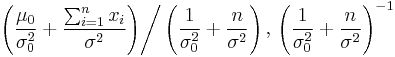 |
| Normal with known precision τ |
μ (mean) | Normal | 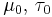 |
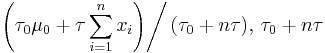 |
| Normal with known mean μ |
σ2 (variance) | Scaled inverse chi-squared | 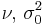 |
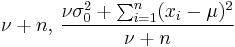 |
| Normal with known mean μ |
τ (precision) | Gamma | 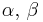 [4] [4] |
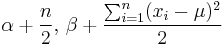 |
| Normal with known mean μ |
σ2 (variance) | Inverse Gamma Distribution | 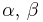 [5] [5] |
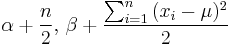 |
| Normal | μ and σ2 Assuming exchangeability |
Normal-scaled inverse gamma | 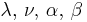 |
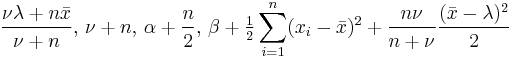 , where , where 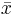 is the sample mean. is the sample mean. |
| Normal | μ and τ Assuming exchangeability |
Normal-gamma | 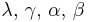 |
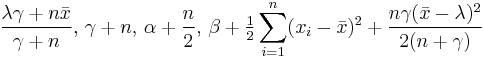 , where , where 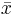 is the sample mean. is the sample mean. |
| Multivariate normal with known covariance matrix | μ (mean vector) | Multivariate normal | 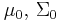 |
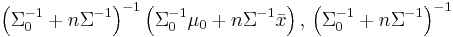 , where , where 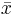 is the sample mean. is the sample mean. |
| Multivariate normal with known precision matrix | μ (mean vector) | Multivariate normal | 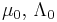 |
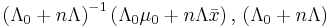 , where , where 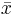 is the sample mean. is the sample mean. |
| Multivariate normal with known mean | Σ (covariance matrix) | Inverse-Wishart | 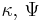 |
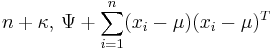 |
| Multivariate normal with known mean | Λ (precision matrix) | Wishart | ||
| Multivariate normal | μ (mean vector) and Σ (covariance matrix) | Normal-Inverse-Wishart distribution | 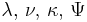 |
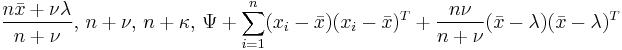 , where , where 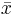 is the sample mean is the sample mean |
| Multivariate normal | μ (mean vector) and Λ (precision matrix) | Normal-Wishart | 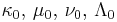 |
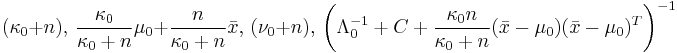 where where 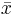 is the sample mean and is the sample mean and 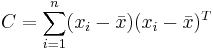 . . |
| Pareto | k (shape) | Gamma | 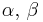 |
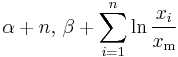 |
| Gamma with known shape α |
β (inverse scale) | Gamma | 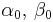 |
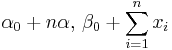 |
| Inverse Gamma with known shape α |
β (inverse scale) | Gamma | 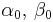 |
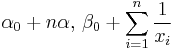 |
| Gamma [6] | α (shape), β (inverse scale) | 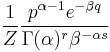 |
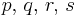 |
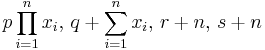 |
References
- ^ Howard Raiffa and Robert Schlaifer. Applied Statistical Decision Theory. Division of Research, Graduate School of Business Administration, Harvard University, 1961.
- ^ Jeff Miller et al. Earliest Known Uses of Some of the Words of Mathematics, "conjugate prior distributions". Electronic document, revision of November 13, 2005, retrieved December 2, 2005.
- ^ Andrew Gelman, John B. Carlin, Hal S. Stern, and Donald B. Rubin. Bayesian Data Analysis, 2nd edition. CRC Press, 2003. ISBN 1-58488-388-X.
- ^ a b c β is rate or inverse scale. In parameterization of Gamma distribution,θ = 1/β and k = α.
- ^ In terms of the Inverse Gamma,
 is a Scale parameter
is a Scale parameter - ^ Fink, D. 1995 A Compendium of Conjugate Priors. In progress report: Extension and enhancement of methods for setting data quality objectives. (DOE contract 95‑831).