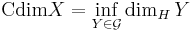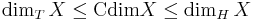Conformal dimension

In mathematics, the conformal dimension of a metric space X is the infimum of the Hausdorff dimension over the conformal gauge of X, that is, the class of all metric spaces quasisymmetric to X.^[1]

1 Formal definition
2 Properties
3 Examples
4 See also
5 References

Formal definition

Let X be a metric space and 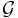$\mathcal{G}$ be the collection of all metric spaces that are quasisymmetric to X. The conformal dimension of X is defined as such

$\mathrm{Cdim} X = \inf_{Y \in \mathcal{G}} \dim_H Y$

Properties

We have the following inequalities, for a metric space X:

$\dim_T X \leq \mathrm{Cdim} X \leq \dim_H X$

The second inequality is true by definition. The first one is deduced from the fact that the topological dimension is invariant by homeomorphism, and thus can be defined as the infimum of the Hausdorff dimension over all spaces homeomorphic to X.

Examples

The conformal dimension of 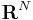$\mathbf{R}^N$ is N, since the topological and Hausdorff dimensions of Euclidean spaces agree.

The Cantor set K is of null conformal dimension. However, there is no metric space quasisymmetric to K with a 0 Hausdorff dimension.

References

^ John M. Mackay, Jeremy T. Tyson, Conformal Dimension : Theory and Application, University Lecture Series, Vol. 54, 2010, Rhodes Island

Conformal dimension

Contents

Formal definition

Properties

Examples

See also

References