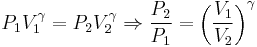Compression ratio
The 'compression ratio' of an internal-combustion engine or external combustion engine is a value that represents the ratio of the volume of its combustion chamber from its largest capacity to its smallest capacity. It is a fundamental specification for many common combustion engines.
In a piston engine it is the ratio between the volume of the cylinder and combustion chamber when the piston is at the bottom of its stroke, and the volume of the combustion chamber when the piston is at the top of its stroke.[1]
Picture a cylinder and its combustion chamber with the piston at the bottom of its stroke containing 1000 cc of air (900 cc in the cylinder plus 100 cc in the combustion chamber). When the piston has moved up to the top of its stroke inside the cylinder, and the remaining volume inside the head or combustion chamber has been reduced to 100 cc, then the compression ratio would be proportionally described as 1000:100, or with fractional reduction, a 10:1 compression ratio.
A high compression ratio is desirable because it allows an engine to extract more mechanical energy from a given mass of air-fuel mixture due to its higher thermal efficiency. High ratios place the available oxygen and fuel molecules into a reduced space along with the adiabatic heat of compression–causing better mixing and evaporation of the fuel droplets. Thus they allow increased power at the moment of ignition and the extraction of more useful work from that power by expanding the hot gas to a greater degree.
Higher compression ratios will however make gasoline engines subject to engine knocking if lower octane-rated fuel is used, also known as detonation. This can reduce efficiency or damage the engine if knock sensors are not present to retard the timing. However, knock sensors have been a requirement of the OBD-II specification used in 1996 model year vehicles and newer.
Diesel engines on the other hand operate on the principle of compression ignition, so that a fuel which resists autoignition will cause late ignition which will also lead to engine knock.
Contents |
Formula
The ratio is calculated by the following formula:
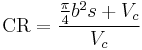 , where
, where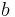 = cylinder bore (diameter)
= cylinder bore (diameter) = piston stroke length
= piston stroke length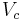 = clearance volume. It is the volume of the combustion chamber (including head gasket). This is the minimum volume of the space at the end of the compression stroke, i.e. when the piston reaches top dead center (TDC). Because of the complex shape of this space, it is usually measured directly rather than calculated.
= clearance volume. It is the volume of the combustion chamber (including head gasket). This is the minimum volume of the space at the end of the compression stroke, i.e. when the piston reaches top dead center (TDC). Because of the complex shape of this space, it is usually measured directly rather than calculated.
Typical compression ratios
Petrol (gasoline) engine
Due to pinging (detonation), the compression ratio in a gasoline or petrol-powered engine will usually not be much higher than 10:1, although some production automotive engines built for high-performance from 1955–1972 had compression ratios as high as 13.0:1, which could run safely on the high-octane leaded gasoline then available.
A technique used to prevent the onset of knock is the high "swirl" engine that forces the intake charge to adopt a very fast circular rotation in the cylinder during compression that provides quicker and more complete combustion. Recently, with the addition of variable valve timing and knock sensors to delay ignition timing, it is possible to manufacture gasoline engines with compression ratios of over 11:1 that can use 87 (MON + RON)/2 (octane rating) fuel.
In engines with a 'ping' or 'knock' sensor and an electronic control unit, the CR can be as high as 13:1 (2005 BMW K1200S). In 1981, Jaguar released a cylinder head that allowed up to 14:1 compression; but settled for 12.5:1 in production cars. The cylinder head design was known as the "May Fireball" head; it was developed by a Swiss engineer Michael May.
Mazda is in 2012 releasing new petrol engines under the brand name SkyActiv with 14:1 compression ratio, to be used in all Mazda vehicles by 2015.[2][3][4]
Petrol/gasoline engine with pressure-charging
In a turbocharged or supercharged gasoline engine, the CR is customarily built at 10.5:1 or lower. This is due to the turbocharger/supercharger already having compressed the fuel/air mixture considerably before it enters the cylinders.
Petrol/gasoline engine for racing
Motorcycle racing engines can use compression ratios as high as 14:1, and it is not uncommon to find motorcycles with compression ratios above 12.0:1 designed for 86 or 87 octane fuel. F1 engines come closer to 17:1 (which is very critical for maximizing volumetric/fuel efficiency at around 18000 rpm)
Ethanol and methanol engines
Ethanol and methanol can take significantly higher compression ratios than gasoline. Racing engines burning methanol and ethanol fuel often incorporate a CR of 14.5-16:1.
Gas-fueled engine
In engines running exclusively on LPG or CNG, the CR may be higher, due to the higher octane rating of these fuels.
Diesel engine
In an auto-ignition diesel engine, there is no electrical sparking plug; the heat of compression raises the temperature of the mixture to its auto-ignition point. The CR will customarily exceed 14:1 and ratios over 22:1 are common. The appropriate compression ratio depends on the design of the cylinder head. The figure is usually between 14:1 and 16:1 for direct injection engines and between 18:1 and 23:1 for indirect injection engines.
Fault finding and diagnosis
Measuring the compression pressure of an engine, with a pressure gauge connected to the spark plug opening, gives an indication of the engine's state and quality. There is, however, no formula to calculate compression ratio based on cylinder pressure.
If the nominal compression ratio of an engine is given, the pre-ignition cylinder pressure can be estimated using the following relationship:
where  is the cylinder pressure at bottom dead center which is usually at 1 atm,
is the cylinder pressure at bottom dead center which is usually at 1 atm, 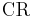 is the compression ratio, and
is the compression ratio, and 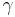 is the specific heat ratio for the working fluid, which is about 1.4 for air, and 1.3 for methane-air mixture.
is the specific heat ratio for the working fluid, which is about 1.4 for air, and 1.3 for methane-air mixture.
For example, if an engine running on gasoline has a compression ratio of 10:1, the cylinder pressure at top dead center is
This figure, however, will also depend on cam (i.e. valve) timing. Generally, cylinder pressure for common automotive designs should at least equal 10 bar, or, roughly estimated in pounds per square inch (psi) as between 15 and 20 times the compression ratio, or in this case between 150 psi and 200 psi, depending on cam timing. Purpose-built racing engines, stationary engines etc. will return figures outside this range.
Factors including late intake valve closure (relatively speaking for camshaft profiles outside of typical production car range, but not necessarily into the realm of competition engines) can produce a misleadingly low figure from this test. Excessive connecting rod clearance, combined with extremely high oil pump output (rare but not impossible) can sling enough oil to coat the cylinder walls with enough oil to facilitate reasonable piston ring seal artificially give a misleadingly high figure, on engines with compromised ring seal.
This can actually be used to some slight advantage. If a compression test does give a low figure, and it has been determined it is not due to intake valve closure/camshaft characteristics, then one can differentiate between the cause being valve/seat seal issues and ring seal by squirting engine oil into the spark plug orifice, in a quantity sufficient to disperse across the piston crown and the circumference of the top ring land, and thereby effect the mentioned seal. If a second compression test is performed shortly thereafter, and the new reading is much higher, it would be the ring seal that is problematic, whereas if the compression test pressure observed remains low, it is a valve sealing (or more rarely head gasket, or breakthrough piston or rarer still cylinder wall damage) issue.
If there is a significant (greater than 10%) difference between cylinders, that may be an indication that valves or cylinder head gaskets are leaking, piston rings are worn or that the block is cracked.
If a problem is suspected then a more comprehensive test using a leak-down tester can locate the leak.
Variable Compression Ratio (VCR) engines
Because cylinder bore diameter, piston stroke length and combustion chamber volume are almost always constant, the compression ratio for a given engine is almost always constant, until engine wear takes its toll.
One exception is the experimental Saab Variable Compression engine (SVC). This engine, designed by Saab Automobile, uses a technique that dynamically alters the volume of the combustion chamber (Vc), which, via the above equation, changes the compression ratio (CR).
The Atkinson cycle engine was one of the first attempts at variable compression. Since the compression ratio is the ratio between dynamic and static volumes of the combustion chamber the Atkinson cycle's method of increasing the length of the powerstroke compared to the intake stroke ultimately altered the compression ratio at different stages of the cycle.
Dynamic compression ratio
The calculated compression ratio, as given above, presumes that the cylinder is sealed at the bottom of the stroke, and that the volume compressed is the actual volume.
However: intake valve closure (sealing the cylinder) always takes place after BDC, which may cause some of the intake charge to be compressed backwards out of the cylinder by the rising piston at very low speeds; only the percentage of the stroke after intake valve closure is compressed. Intake port tuning and scavenging may allow a greater mass of charge (at a higher than atmospheric pressure) to be trapped in the cylinder than the static volume would suggest ( This "corrected" compression ratio is commonly called the "dynamic compression ratio".
This ratio is higher with more conservative (i.e., earlier, soon after BDC) intake cam timing, and lower with more radical (i.e., later, long after BDC) intake cam timing, but always lower than the static or "nominal" compression ratio.
The actual position of the piston can be determined by trigonometry, using the stroke length and the connecting rod length (measured between centers). The absolute cylinder pressure is the result of an exponent of the dynamic compression ratio. This exponent is a polytropic value for the ratio of variable heats for air and similar gases at the temperatures present. This compensates for the temperature rise caused by compression, as well as heat lost to the cylinder. Under ideal (adiabatic) conditions, the exponent would be 1.4, but a lower value, generally between 1.2 and 1.3 is used, since the amount of heat lost will vary among engines based on design, size and materials used, but provides useful results for purposes of comparison. For example, if the static compression ratio is 10:1, and the dynamic compression ratio is 7.5:1, a useful value for cylinder pressure would be (7.5)^1.3 × atmospheric pressure, or 13.7 bar. (× 14.7 psi at sea level = 201.8 psi. The pressure shown on a gauge would be the absolute pressure less atmospheric pressure, or 187.1 psi.)
The two corrections for dynamic compression ratio affect cylinder pressure in opposite directions, but not in equal strength. An engine with high static compression ratio and late intake valve closure will have a DCR similar to an engine with lower compression but earlier intake valve closure.
Additionally, the cylinder pressure developed when an engine is running will be higher than that shown in a compression test for several reasons.
- The much higher velocity of a piston when an engine is running versus cranking allows less time for pressure to bleed past the piston rings into the crankcase.
- a running engine is coating the cylinder walls with much more oil than an engine that is being cranked at low RPM, which helps the seal.
- the higher temperature of the cylinder will create higher pressures when running vs. a static test, even a test performed with the engine near operating temperature.
- A running engine does not stop taking air & fuel into the cylinder when the piston reaches BDC; The mixture that is rushing into the cylinder during the downstroke develops momentum and continues briefly after the vacuum ceases (in the same respect that rapidly opening a door will create a draft that continues after movement of the door ceases). This is called scavenging. Intake tuning, cylinder head design, valve timing and exhaust tuning determine how effectively an engine scavenges.
Compression ratio versus overall pressure ratio
Compression ratio and overall pressure ratio are interrelated as follows:
| Compression ratio | 2:1 | 3:1 | 5:1 | 10:1 | 15:1 | 20:1 | 25:1 | 35:1 |
|---|---|---|---|---|---|---|---|---|
| Pressure ratio | 2.64:1 | 4.66:1 | 9.52:1 | 25.12:1 | 44.31:1 | 66.29:1 | 90.60:1 | 145.11:1 |
The reason for this difference is that compression ratio is defined via the volume reduction:
 ,
,
while pressure ratio is defined as the pressure increase:
 .
.
In calculating the pressure ratio, we assume that an adiabatic compression is carried out (i.e. that no heat energy is supplied to the gas being compressed, and that any temperature rise is solely due to the compression). We also assume that air is a perfect gas. With those two assumptions we can define the relationship between change of volume and change of pressure as follows:
where  is the ratio of specific heats for air (approximately 1.4). The values in the table above are derived using this formula. Note that in reality the ratio of specific heats changes with temperature and that significant deviations from adiabatic behavior will occur.
is the ratio of specific heats for air (approximately 1.4). The values in the table above are derived using this formula. Note that in reality the ratio of specific heats changes with temperature and that significant deviations from adiabatic behavior will occur.
See also
- Mean effective pressure
- Overall pressure ratio - a closely related ratio for jet engines
Notes
- ^ Encyclopædia Britannica, Compression ratio, http://www.britannica.com/EBchecked/topic/130313/compression-ratio, retrieved 2009-07-21
- ^ http://www.autoweek.com/article/20110422/NEWYORK/110429942
- ^ http://reviews.cnet.com/8301-13746_7-20015698-48.html
- ^ http://www.caranddriver.com/news/mazda-engine-news-mazda-sky-gas-and-diesel-details-car-and-driver
External links
- "Here Comes High Compression Engines " 1949 highly detailed article in Popular Science with photos and cutaway drawings
- Variable compression engine
- Cam Timing vs. Compression Ratio Analysis
- Calculating Compression Ratio changes with engine modifications
In:Hindi