Completeness

In general, an object is complete if nothing needs to be added to it. This notion is made more specific in various fields.

Contents 1 Logical completeness 2 Mathematical completeness 3 Computing 4 Economics, finance, and industry 5 Botany 6 References

Logical completeness

In logic, semantic completeness is the converse of soundness for formal systems. A formal system is "semantically complete" when all its tautologies are theorems, whereas a formal system is "sound" when all theorems are tautologies (that is, they are semantically valid formulas: formulas that are true under every interpretation of the language of the system that is consistent with the rules of the system). Kurt Gödel, Leon Henkin, and Emil Post all published proofs of completeness. (See History of the Church–Turing thesis.) A formal system is consistent if for all formulas φ of the system, the formulas φ and ¬φ (the negation of φ) are not both theorems of the system (that is, they cannot be both proved with the rules of the system).

• A formal system S is semantically complete or simply complete, if and only if every tautology of S is a theorem of S. That is, 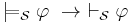.^[1]

• A formal system S is strongly complete or complete in the strong sense if and only if for every set of premises Γ, any formula which semantically follows from Γ is derivable from Γ. That is, .

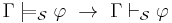• A formal system S is syntactically complete or deductively complete or maximally complete or simply complete if and only if for each formula φ of the language of the system either φ or ¬φ is a theorem of S. This is also called negation completeness. In another sense, a formal system is syntactically complete if and only if no unprovable axiom can be added to it as an axiom without introducing an inconsistency. Truth-functional propositional logic and first-order predicate logic are semantically complete, but not syntactically complete (for example, the propositional logic statement consisting of a single variable "a" is not a theorem, and neither is its negation, but these are not tautologies). Gödel's incompleteness theorem shows that any recursive system that is sufficiently powerful, such as Peano arithmetic, cannot be both consistent and complete.

• A formal system is inconsistent if and only if every sentence is a theorem.^[2]

• A system of logical connectives is functionally complete if and only if it can express all propositional functions.

• A language is expressively complete if it can express the subject matter for which it is intended.

• A formal system is complete with respect to a property if and only if every sentence that has the property is a theorem.

Mathematical completeness

In mathematics, "complete" is a term that takes on specific meanings in specific situations, and not every situation in which a type of "completion" occurs is called a "completion". See, for example, algebraically closed field or compactification.

• The completeness of the real numbers is one of the defining properties of the real number system. It may be described equivalently as either the completeness of R as metric space or as a partially ordered set (see below).

• A metric space is complete if every Cauchy sequence in it converges. See Complete metric space.

• A uniform space is complete if every Cauchy net in it converges (or equivalently every Cauchy filter in it converges).

• In functional analysis, a subset S of a topological vector space V is complete if its span is dense in V. In the particular case of Hilbert spaces (or more generally, inner product spaces), an orthonormal basis is a set that is both complete and orthonormal.

• A measure space is complete if every subset of every null set is measurable. See complete measure.

• In commutative algebra, a commutative ring can be completed at an ideal (in the topology defined by the powers of the ideal). See Completion (ring theory).

• More generally, any topological group can be completed at a decreasing sequence of open subgroups.

• In statistics, a statistic is called complete if it does not allow an unbiased estimator of zero. See completeness (statistics).

• In graph theory, a complete graph is an undirected graph in which every pair of vertices has exactly one edge connecting them.

• In category theory, a category C is complete if every diagram from a small category to C has a limit; it is cocomplete if every such functor has a colimit.

• In order theory and related fields such as lattice and domain theory, completeness generally refers to the existence of certain suprema or infima of some partially ordered set. Notable special usages of the term include the concepts of complete Boolean algebra, complete lattice, and complete partial order (cpo). Furthermore, an ordered field is complete if every non-empty subset of it that has an upper bound within the field has a least upper bound within the field, which should be compared to the (slightly different) order-theoretical notion of bounded completeness. Up to isomorphism there is only one complete ordered field: the field of real numbers (but note that this complete ordered field, which is also a lattice, is not a complete lattice).

• In algebraic geometry, an algebraic variety is complete if it satisfies an analog of compactness. See complete algebraic variety.

• In quantum mechanics, a complete set of commuting operators (or CSCO) is one whose eigenvalues are sufficient to specify the physical state of a system.

Computing

• In algorithms, the notion of completeness refers to the ability of the algorithm to find a solution if one exists, and if not, to report that no solution is possible.
• In computational complexity theory, a problem P is complete for a complexity class C, under a given type of reduction, if P is in C, and every problem in C reduces to P using that reduction. For example, each problem in the class NP-complete is complete for the class NP, under polynomial-time, many-one reduction.
• In computing, a data-entry field can autocomplete the entered data based on the prefix typed into the field; that capability is known as autocompletion.
• In software testing, completeness has for goal the functional verification of call graph (between software item) and control graph (inside each software item).
• The concept of completeness is found in knowledge base theory.

Economics, finance, and industry

• Complete markets versus incomplete markets
• In auditing, completeness is one of the financial statement assertions that have to be ensured. For example, auditing classes of transactions. Rental expense which includes 12-month or 52-week payments should be all booked according to the terms agreed in the tenancy agreement.
• Oil or gas well completion, the process of making a well ready for production.

Botany

• A complete flower is a flower with both male and female reproductive structures as well as petals and sepals. See Sexual reproduction in plants.

References

Logic   Overview Academic areas Argumentation theory Axiology Critical thinking Computability theory Formal semantics History of logic Informal logic Logic in computer science Mathematical logic Mathematics Metalogic Metamathematics Model theory Philosophical logic Philosophy Philosophy of logic Philosophy of mathematics Proof theory Set theory Foundational concepts Abduction Analytic truth Antinomy A priori Deduction Definition Description Entailment Induction Inference Logical consequence Logical form Logical implication Logical truth Name Necessity Meaning Paradox Possible world Presupposition Probability Reason Reasoning Reference Semantics Statement Strict implication Substitution Syntax Truth Truth value Validity   Philosophical logic Critical thinking and Informal logic Analysis Ambiguity Argument Belief Bias Credibility Evidence Explanation Explanatory power Fact Fallacy Inquiry Opinion Parsimony Premise Propaganda Prudence Reasoning Relevance Rhetoric Rigor Vagueness Theories of deduction Constructivism Dialetheism Fictionalism Finitism Formalism Intuitionism Logical atomism Logicism Nominalism Platonic realism Pragmatism Realism   Metalogic and metamathematics Cantor's theorem Church's theorem Church's thesis Consistency Effective method Foundations of mathematics Gödel's completeness theorem Gödel's incompleteness theorems Soundness Completeness Decidability Interpretation Löwenheim–Skolem theorem Metatheorem Satisfiability Independence Type–token distinction Use–mention distinction   Mathematical logic General Formal language Formation rule Formal system Deductive system Formal proof Formal semantics Well-formed formula Set Element Class Classical logic Axiom Natural deduction Rule of inference Relation Theorem Logical consequence Axiomatic system Type theory Symbol Syntax Theory Traditional logic Proposition Inference Argument Validity Cogency Syllogism Square of opposition Venn diagram Propositional calculus and Boolean logic Boolean functions Propositional calculus Propositional formula Logical connectives Truth tables Predicate First-order Quantifiers Predicate Second-order Monadic predicate calculus Set theory Set Empty set Enumeration Extensionality Finite set Function Subset Power set Countable set Recursive set Domain Range Ordered pair Uncountable set Model theory Model Interpretation Non-standard model Finite model theory Truth value Validity Proof theory Formal proof Deductive system Formal system Theorem Logical consequence Rule of inference Syntax Computability theory Recursion Recursive set Recursively enumerable set Decision problem Church–Turing thesis Computable function Primitive recursive function   Non-classical logic Modal logic Alethic Axiologic Deontic Doxastic Epistemic Temporal Intuitionism Intuitionistic logic Constructive analysis Heyting arithmetic Intuitionistic type theory Constructive set theory Fuzzy logic Degree of truth Fuzzy rule Fuzzy set Fuzzy finite element Fuzzy set operations Substructural logic Structural rule Relevance logic Linear logic Paraconsistent logic Dialetheism Description logic Ontology Ontology language   Logicians Anderson Aristotle Averroes Avicenna Bain Barwise Bernays Boole Boolos Cantor Carnap Church Chrysippus Curry De Morgan Frege Geach Gentzen Gödel Hilbert Kleene Kripke Leibniz Löwenheim Peano Peirce Putnam Quine Russell Schröder Scotus Skolem Smullyan Tarski Turing Whitehead William of Ockham Wittgenstein Zermelo   Lists Topics Outline of logic Index of logic articles Mathematical logic Boolean algebra Set theory Other Logicians Rules of inference Paradoxes Fallacies Logic symbols Portal Category Outline WikiProject Talk changes