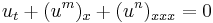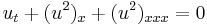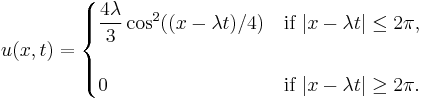Compacton

In the theory of integrable systems, a compacton, introduced in (Philip Rosenau & James M. Hyman 1993), is a soliton with compact support.

An example of an equation with compacton solutions is the generalization

u_t%2B(u^m)_x%2B(u^n)_{xxx}=0\,

of the Korteweg–de Vries equation with m, n > 1. (The case when m = 2, n = 1 is essentially the KdV equation.)

Example

The equation

u_t%2B(u^2)_x%2B(u^2)_{xxx}=0 \,

has a travelling wave solution given by

u(x,t) = \begin{cases} \dfrac{4\lambda}{3}\cos^2((x-\lambda t)/4) & \text{if }|x - \lambda t| \le 2\pi, \\ \\ 0 & \text{if }|x - \lambda t| \ge 2\pi. \end{cases}

This has compact support in x, so is a compacton.

See also

References