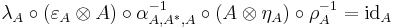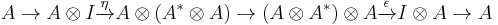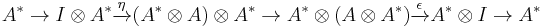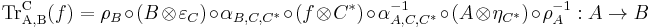Compact closed category
In category theory, compact closed categories are a general context for treating dual objects. The idea of a dual object generalizes the more familiar concept of the dual of a finite-dimensional vector space. So, the motivating example of a compact closed category is FdVect, the category with finite dimensional vector spaces as objects and linear maps as morphisms.
Contents |
Definition
A symmetric monoidal category 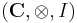 is compact closed if every object
is compact closed if every object 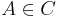 has a dual object. If this holds, the dual object is unique up to canonical isomorphism, and it is denoted
has a dual object. If this holds, the dual object is unique up to canonical isomorphism, and it is denoted 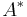 .
.
In a bit more detail, an object 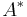 is called the dual of A if it is equipped with two morphisms called the unit
is called the dual of A if it is equipped with two morphisms called the unit 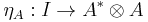 and the counit
and the counit 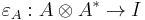 , satisfying the equations
, satisfying the equations
and
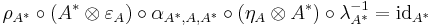 .
.
For clarity, we rewrite the above compositions diagramatically:
and
Properties
Compact closed categories are a special case of monoidal closed categories, which in turn are a special case of closed categories.
Compact closed categories are precisely the symmetric autonomous categories. They are also *-autonomous.
Every compact closed category C admits a trace. Namely, for every morphism 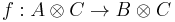 , one can define
, one can define
which can be shown to be a proper trace.
Examples
The canonical example is the category FdVect with finite dimensional vector spaces as objects and linear maps as morphisms. Here 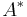 is the usual dual of the vector space
is the usual dual of the vector space  .
.
The category of finite-dimensional representations of any group is also compact closed.
The category Vect, with all vector spaces as objects and linear maps as morphisms, is not compact closed.
References
Kelly, G.M.; Laplaza, M.L. (1980). "Coherence for compact closed categories". Journal of Pure and Applied Algebra 19: 193–213. doi:10.1016/0022-4049(80)90101-2.