Combs method
The Combs method is a method of writing fuzzy logic rules described by William E. Combs in 1997. It is designed to prevent combinatorial explosion in fuzzy logic rules.
The Combs method takes advantage of the logical equality 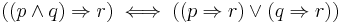 .
.
Contents |
Equality proof
The simplest proof of given equality involves usage of truth tables:
 |
 |
 |
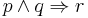 |
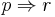 |
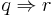 |
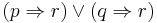 |
|---|---|---|---|---|---|---|
| T | T | T | T | T | T | T |
| T | T | N | F | F | F | F |
| T | F | T | T | T | T | T |
| T | F | F | T | F | T | T |
| F | T | T | T | T | T | T |
| F | T | F | T | T | F | T |
| F | F | T | T | T | T | T |
| F | F | F | T | T | T | T |
Combinatorial explosion
Suppose we have a fuzzy system that considers N variables at a time, each of which can fit into at least one of S sets. The number of rules necessary to cover all the cases in a traditional fuzzy system is 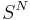 , whereas the Combs method would need only
, whereas the Combs method would need only 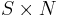 rules. For example, if we have five sets and five variables to consider to produce one output, covering all the cases would require 3125 rules in a traditional system, while the Combs method would require only 25 rules, taming the combinatorial explosion that occurs when more inputs or more sets are added to the system.
rules. For example, if we have five sets and five variables to consider to produce one output, covering all the cases would require 3125 rules in a traditional system, while the Combs method would require only 25 rules, taming the combinatorial explosion that occurs when more inputs or more sets are added to the system.
This article will focus on the Combs method itself. To learn more about the way rules are traditionally formed, see fuzzy logic and fuzzy associative matrix.
Example
Suppose we were designing an artificial personality system that determined how friendly the personality is supposed to be towards a person in a strategic video game. The personality would consider its own fear, trust, and love in the other person. A set of rules in the Combs system might look like this:
| Fear | Unafraid THEN Enemies | Moderate Fear THEN Neutral | Afraid THEN Good Friends |
|---|---|---|---|
| Trust | Distrusting THEN Enemies | Moderate Trust THEN Neutral | Trusting THEN Good Friends |
| Love | Unloving THEN Enemies | Moderate Love THEN Neutral | Loving THEN Good Friends |
The table translates to:
[IF Fear IS Unafraid THEN Friendship IS Enemies OR IF Fear IS ModerateFear THEN Friendship IS Neutral OR IF Fear IS Afraid THEN Friendship IS GoodFriends ] OR [IF Trust IS Distrusting THEN Friendship IS Enemies OR IF Trust IS ModerateTrust THEN Friendship IS Neutral OR IF Trust IS Trusting THEN Friendship IS GoodFriends] OR [IF Love IS Unloving THEN Friendship IS Enemies OR IF Love IS ModerateLove THEN Friendship IS Neutral OR IF Love IS Loving THEN Friendship IS GoodFriends]
In this case, because the table follows a straightforward pattern in the output, it could be rewritten as:
| Fear | Unafraid | Moderate Fear | Afraid |
|---|---|---|---|
| Trust | Distrusting | Moderate Trust | Trusting |
| Love | Unloving | Moderate Love | Loving |
| Friendship | Enemies | Neutral | Good Friends |
Each column of the table maps to the output provided in the last row. To obtain the output of the system, we just average the outputs of each rule for that output. For example, to calculate how much the computer is Enemies with the player, we take the average of how much the computer is Unafraid, Distrusting, and Unloving of the player. When all three averages are obtained, the result can then be defuzzified by any of the traditional means.
References
- The Combs Method for Rapid Inference (the original paper by William E. Combs)