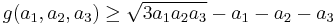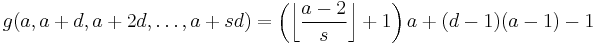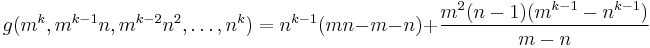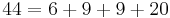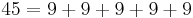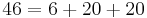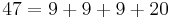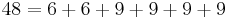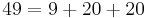Coin problem

The coin problem (also referred to as the Frobenius coin problem or Frobenius problem, after the mathematician Ferdinand Frobenius) is a mathematical problem that asks what is the largest monetary amount that cannot be obtained using only coins of specified denominations.[1] For example, the largest amount that cannot be obtained using only coins of 3 and 5 units is 7 units. The solution to this problem for a given set of coin denominations is called the Frobenius number of the set.

There is an explicit formula for the Frobenius number when there are only two different coin denominations. If the number of coin denominations is three or more, no explicit formula is known; but, for any fixed number of coin denominations, there is an algorithm computing the Frobenius number in polynomial time (in the logarithms of the coin denominations forming an input).[2] No known algorithm is polynomial time in the number of coin denominations, and the general problem, where the number of coin denominations may be as large as desired, is NP-hard.[3][4]

Contents

Statement

In mathematical terms the problem can be stated:

Given positive integers a1, a2, ..., an such that gcd(a1, a2, ..., an) = 1, find the largest integer that cannot be expressed as an integer conical combination of these numbers, i.e., as a sum
k1a1 + k2a2 + ··· + knan,
where k1, k2, ..., kn are non-negative integers.

This largest integer is called the Frobenius number of the set { a1, a2, ..., an }, and is usually denoted by g(a1, a2, ..., an).

The requirement that the greatest common divisor (GCD) equal 1 is necessary in order for the Frobenius number to exist. If the GCD were not 1, every integer that is not a multiple of the GCD would be inexpressible as a linear, let alone conical, combination of the set, and therefore there would not be a largest such number. For example, if you had two types of coins valued at 4 cents and 6 cents, the GCD would equal 2, and there would be no way to combine any number of such coins to produce a sum which was an odd number. On the other hand, whenever the GCD equals 1, the set of integers that cannot be expressed as a conical combination of { a1, a2, ..., an } is bounded according to Schur's theorem, and therefore the Frobenius number exists.

Frobenius numbers for small n

A closed-form solution exists for the coin problem only where n = 1 or 2. No closed-form solution is known for n > 2.[4]

n = 1

If n = 1, then a1 = 1 so that all natural numbers can be formed. Hence no Frobenius number in one variable exists.

n = 2

If n = 2, the Frobenius number can be found from the formula 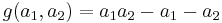g(a_1, a_2) = a_1a_2-a_1-a_2. This formula was discovered by James Joseph Sylvester in 1884.[5] Sylvester also demonstrated for this case that there are a total of 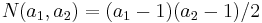N(a_1, a_2) = (a_1-1)(a_2-1)/2 non-representable integers.

n = 3

Fast algorithms are known for three numbers, though the calculations can be very tedious if done by hand. Furthermore, lower- and upper bounds for the n = 3 Frobenius numbers have been determined. The Frobenius-type lower bound due to Davidson

g(a_1, a_2, a_3) \geq \sqrt{3a_1a_2a_3} - a_1 - a_2 - a_3

is reported to be relatively sharp.[6]

Frobenius numbers for special sets

Arithmetic sequences

A simple formula exists for the Frobenius number of a set of integers in arithmetic sequence.[7] Given integers a, d, s with gcd(a, d) = 1:

g(a,a%2Bd,a%2B2d,\dots,a%2Bsd)=\left(\left\lfloor\frac{a-2}{s}\right\rfloor%2B1\right)a%2B(d-1)(a-1)-1

Geometric sequences

There also exists a closed form solution for the Frobenius number of a set in geometric sequence.[8] Given integers m, n, k with gcd(m, n) = 1:

g(m^k,m^{k-1}n,m^{k-2}n^2,\dots,n^k)=n^{k-1}(mn-m-n)%2B\frac{m^2(n-1)(m^{k-1}-n^{k-1})}{m-n}

Examples

McNugget numbers

One special case of the coin problem is sometimes also referred to as the McNugget numbers. The McNuggets version of the coin problem was introduced by Henri Picciotto, who included it in his algebra textbook co-authored with Anita Wah.[9] Picciotto thought of the application in the 1980s while dining with his son at McDonald's, working the problem out on a napkin. A McNugget number is the total number of McDonald's Chicken McNuggets in any number of boxes. The original boxes (prior to the introduction of the Happy Meal-sized nugget boxes) were of 6, 9, and 20 nuggets.

According to Schur's theorem, since 6, 9, and 20 are relatively prime, any sufficiently large integer can be expressed as a linear combination of these three. Therefore, there exists a largest non-McNugget number, and all integers larger than it are McNugget numbers. Namely, every positive integer is a McNugget number, with the finite number of exceptions:

1, 2, 3, 4, 5, 7, 8, 10, 11, 13, 14, 16, 17, 19, 22, 23, 25, 28, 31, 34, 37, and 43 (sequence A065003 in OEIS).

Thus the largest non-McNugget number is 43.[10] The fact that any integer larger than 43 is a McNugget number can be seen by considering the following integer partitions

44 = 6 %2B 9 %2B 9 %2B 20
45 = 9 %2B 9 %2B 9 %2B 9 %2B 9
46 = 6 %2B 20 %2B 20
47 = 9 %2B 9 %2B 9 %2B 20
48 = 6 %2B 6 %2B 9 %2B 9 %2B 9 %2B 9
49 = 9 %2B 20 %2B 20

implying that any larger integer can obtained by adding some number of 6's to the appropriate partition above.

Furthermore, a straightforward check demonstrates that 43 McNuggets can indeed not be purchased, as:

  1. boxes of 6 and 9 alone can not form 43 as these can only create multiples of 3 (with the exception of 3 itself);
  2. including a single box of 20 does not help, as the required remainder (23) is also not a multiple of 3; and
  3. more than one box of 20, complemented with boxes of size 6 or larger, obviously can not lead to a total of 43 McNuggets.

Other examples

In rugby union, there are four types of scores: penalty goal (3 points), drop goal (3 points), try (5 points) and converted try (7 points). By combining these any points total is possible except 1, 2, or 4.

Similarly, in American football any score is possible in a non-forfeit game except 1. The only ways to score 1 point are by a single point conversion after a 6 point touchdown, or to win by forfeit, where the score will be recorded as 1-0. As 2 points are awarded for a safety and 3 points for a field goal, all other scores apart from 1 are possible.

See also

References

  1. ^ J. Ramírez Alfonsín (2005). The Diophantine Frobenius problem. Oxford Univ. Press. 
  2. ^ Ravi Kannan (1992). "Lattice translates of a polytope and the Frobenius problem". Combinatorica 12 (2): 161–177. doi:10.1007/BF01204720. 
  3. ^ D. Beihoffer, J. Hendry, A. Nijenhuis, and S. Wagon (2005). "Faster algorithms for Frobenius numbers". Electronic Journal of Combinatorics 12: R27. http://www.combinatorics.org/Volume_12/Abstracts/v12i1r27.html. 
  4. ^ a b Weisstein, Eric W., "Coin Problem" from MathWorld.
  5. ^ Sylvester, James Joseph (1884). "Question 7382". Mathematical Questions from the Educational Times 37: 26. 
  6. ^ M. Beck and S. Zacks (2004). "Refined upper bounds for the linear Diophantine problem of Frobenius". Adv. Appl. Math. 32 (3): 454–467. arXiv:math/0305420. doi:10.1016/S0196-8858(03)00055-1. 
  7. ^ Ramirez Alfonsin, Jorge (2005). The Diophantine Frobenius Problem. Oxford University Press. pp. 59–60. 
  8. ^ Ong, Darren C. and Ponomarenko, Vadim (2008). "The Frobenius Number of Geometric Sequences". INTEGERS: the Electronic Journal of Combinatorial Number Theory 8 (1): A33. http://www.emis.ams.org/journals/INTEGERS/papers/i33/i33.Abstract.html. 
  9. ^ A. Wah, H. Picciotto (1994). "Lesson 5.8 Building-block Numbers". Algebra: Themes, Tools, Concepts. p. 186. http://www.mathedpage.org/attc/lessons/ch.05/5.08-building-blocks.pdf. 
  10. ^ Weisstein, Eric W., "McNugget Number" from MathWorld.

External links