Cofunction
This article is about a mathematical term. For an entity in computer science, see Coroutine.
In mathematics, a function f is cofunction of a function g if f(A) = g(B) whenever A and B are complementary angles. This definition typically applies to trigonometric functions.
For example, sine and cosine are cofunctions of each other (hence the "co" in "cosine"):
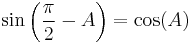 |
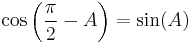 |
The same is true of secant and cosecant and of tangent and cotangent:
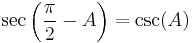 |
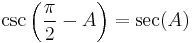 |
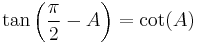 |
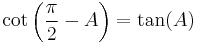 |
Sometimes writing a function in terms of its cofunction helps solve trigonometric equations. A simple example is the equation sin A = cos B.