Cocks IBE scheme
Cocks IBE scheme is an Identity based encryption system proposed by Clifford Cocks in 2001 [1]. The security of the scheme is based on the hardness of the quadratic residuosity problem.
Contents |
Protocol
Setup
The PKG chooses:
- a public RSA-modulus
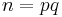 , where
, where 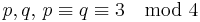 are prime and kept secret,
are prime and kept secret, - the message and the cipher space
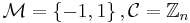 and
and - a secure public hash function
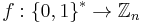 .
.
Extract
When user 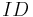 wants to obtain his private key, he contacts the PKG through a secure channel. The PKG
wants to obtain his private key, he contacts the PKG through a secure channel. The PKG
- derives
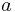 with
with 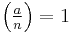 by a determistic process from
by a determistic process from 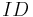 (e.g. multiple application of
(e.g. multiple application of 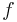 ),
), - computes
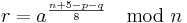 (which fulfils either
(which fulfils either 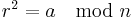 or
or 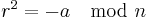 , see below) and
, see below) and - transmits
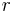 to the user.
to the user.
Encrypt
To encrypt a bit (coded as 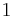 /
/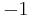 )
) 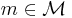 for
for 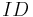 , the user
, the user
- chooses random
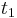 with
with 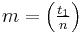 ,
, - chooses random
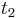 with
with 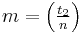 , different from
, different from 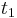 ,
, - computes
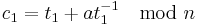 and
and 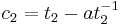 and
and - sends
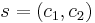 to the user.
to the user.
Decrypt
To decrypt a ciphertext 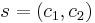 for user
for user 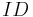 , he
, he
- computes
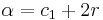 if
if 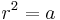 or
or 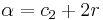 otherwise, and
otherwise, and - computes
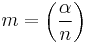 .
.
Note that here we are assuming that the encrypting entity does not know whether 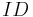 has the square root
has the square root  of
of  or
or 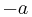 . In this case we have to send a ciphertext for both cases. As soon as this information is known to the encrypting entity, only one element needs to be sent.
. In this case we have to send a ciphertext for both cases. As soon as this information is known to the encrypting entity, only one element needs to be sent.
Correctness
First note that since 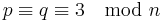 (i.e.
(i.e. 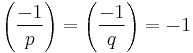 ) and
) and 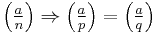 , either
, either 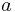 or
or 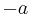 is a quadratic residue modulo
is a quadratic residue modulo 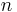 .
.
Therefore, 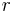 is a square root of
is a square root of 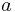 or
or 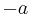 :
:
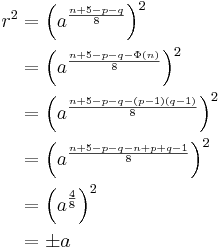
Moreover (for the case that 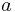 is a quadratic residue, same idea holds for
is a quadratic residue, same idea holds for 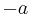 ):
):
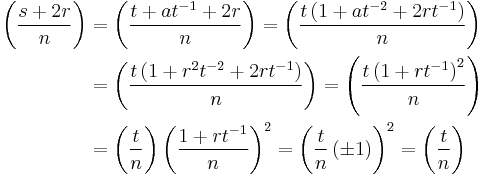
Security
It can be shown that breaking the scheme is equivalent to solving the quadratic residuosity problem , which is suspected to be very hard. The common rules for choosing a RSA modulus hold: Use a secure 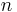 , make the choice of
, make the choice of 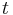 uniform and random and moreover include some authenticity checks for
uniform and random and moreover include some authenticity checks for 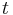 (otherwise, an adaptive chosen ciphertext attack can be mounted by altering packets that transmit a single bit and using the oracle to observe the effect on the decrypted bit).
(otherwise, an adaptive chosen ciphertext attack can be mounted by altering packets that transmit a single bit and using the oracle to observe the effect on the decrypted bit).
Problems
A major disadavantage of this scheme is that it can encrypt messages only bit per bit - therefore, it is only suitable for small data packets like a session key. To illustrate, consider a 128 bit key that is transmitted using a 1024 bit modulus. Then, one has to send 2 * 128 * 1024 bit = 32 KByte (when it is not known whether  is the square of
is the square of  or
or 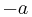 ), which is only acceptable for environments in which session keys change infrequently.
), which is only acceptable for environments in which session keys change infrequently.
This scheme does not preserve key-privacy, i.e. a passive adversary can recover meaningful information about the identity of the recipient observing the ciphertext.
References
- ^ Clifford Cocks, An Identity Based Encryption Scheme Based on Quadratic Residues, Proceedings of the 8th IMA International Conference on Cryptography and Coding, 2001