Circular shift
In combinatorial mathematics, a circular shift is the operation of rearranging the entries in a tuple, either by moving the final entry to the first position, while shifting all other entries to the next position, or by performing the inverse operation. Thus, a circular shift is given by the action of a particular permutation σ of the n positions in the tuple, for which 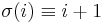 modulo n for all i (or
modulo n for all i (or 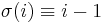 modulo n for the inverse operation). This permutation is a (very particular) instance of an n-cycle.
modulo n for the inverse operation). This permutation is a (very particular) instance of an n-cycle.
The result of repeatedly applying circular shifts to a given tuple are also called the circular shifts of the tuple.
For example, repeatedly applying circular shifts to the 4-tuple (a, b, a, c) successively gives
- (c, a, b, a),
- (a, c, a, b),
- (b, a, c, a),
- (a, b, a, c) (the original 4-tuple),
and then the sequence repeats; this 4-tuple therefore has 4 circular shifts. However the 4-tuple (a, b, a, b) only has 2 (distinct) circular shifts. In general the number of circular shifts of an n-tuple could be any divisor of n, depending on the entries of the tuple.
In computer programming, a circular shift (or bitwise rotation) is a shift operator that shifts all bits of its operand. Unlike an arithmetic shift, a circular shift does not preserve a number's sign bit or distinguish a number's exponent from its mantissa. Unlike a logical shift, the vacant bit positions are not filled in with zeros but are filled in with the bits that are shifted out of the sequence.
Contents |
Implementing circular shifts
Circular shifts are used often in cryptography in order to permute bit sequences. Unfortunately, many programming languages, including C, do not have operators or standard functions for circular shifting, even though several processors have bitwise operation instructions for it (e.g. Intel x86 has ROL and ROR).
Some compilers may provide access to the processor instructions by means of intrinsic functions.
Contrary to popular belief, it is possible to write standard ANSI C code that compiles down to the "rotate" assembly language instruction (on CPUs that have such an instruction).
Most C compilers recognize this idiom:
unsigned int x; unsigned int y; /* ... */ y = (x >> shift) | (x << (sizeof(x)*8 - shift));
and compile it to a single 32 bit rotate instruction.[1][2]
On some systems, this may be "#define"ed as a macro or defined as an inline function called something like "rightrotate32" or "rotr32" or "ror32" in a standard header file like "bitops.h".[3] Rotates in the other direction may be "#define"ed as a macro or defined as an inline function called something like "leftrotate32" or "rotl32" in the same "bitops.h" header file.
If necessary, circular shift functions can be defined (here in C):
unsigned int _rotl(const unsigned int value, int shift) { if ((shift &= sizeof(value)*8 - 1) == 0) return value; return (value << shift) | (value >> (sizeof(value)*8 - shift)); } unsigned int _rotr(const unsigned int value, int shift) { if ((shift &= sizeof(value)*8 - 1) == 0) return value; return (value >> shift) | (value << (sizeof(value)*8 - shift)); }
Example
If the bit sequence 0001 0111 were subjected to a circular shift of one bit position... (see images below)
- to the left would yield: 0010 1110
- to the right would yield: 1000 1011.
If the bit sequence 0001 0111 were subjected to a circular shift of three bit positions...
- to the left would yield: 1011 1000
- to the right would yield: 1110 0010.
Applications
Cyclic codes are a kind of block code with the property that the circular shift of a codeword will always yield another codeword.
See also
References
- ^ GCC: "Optimize common rotate constructs"
- ^ "Cleanups in ROTL/ROTR DAG combiner code" mentions that this code supports the "rotate" instruction in the CellSPU
- ^ "replace private copy of bit rotation routines" -- recommends including "bitops.h" and using its rol32 and ror32 rather than copy-and-paste into a new program.